Tonality structure in music

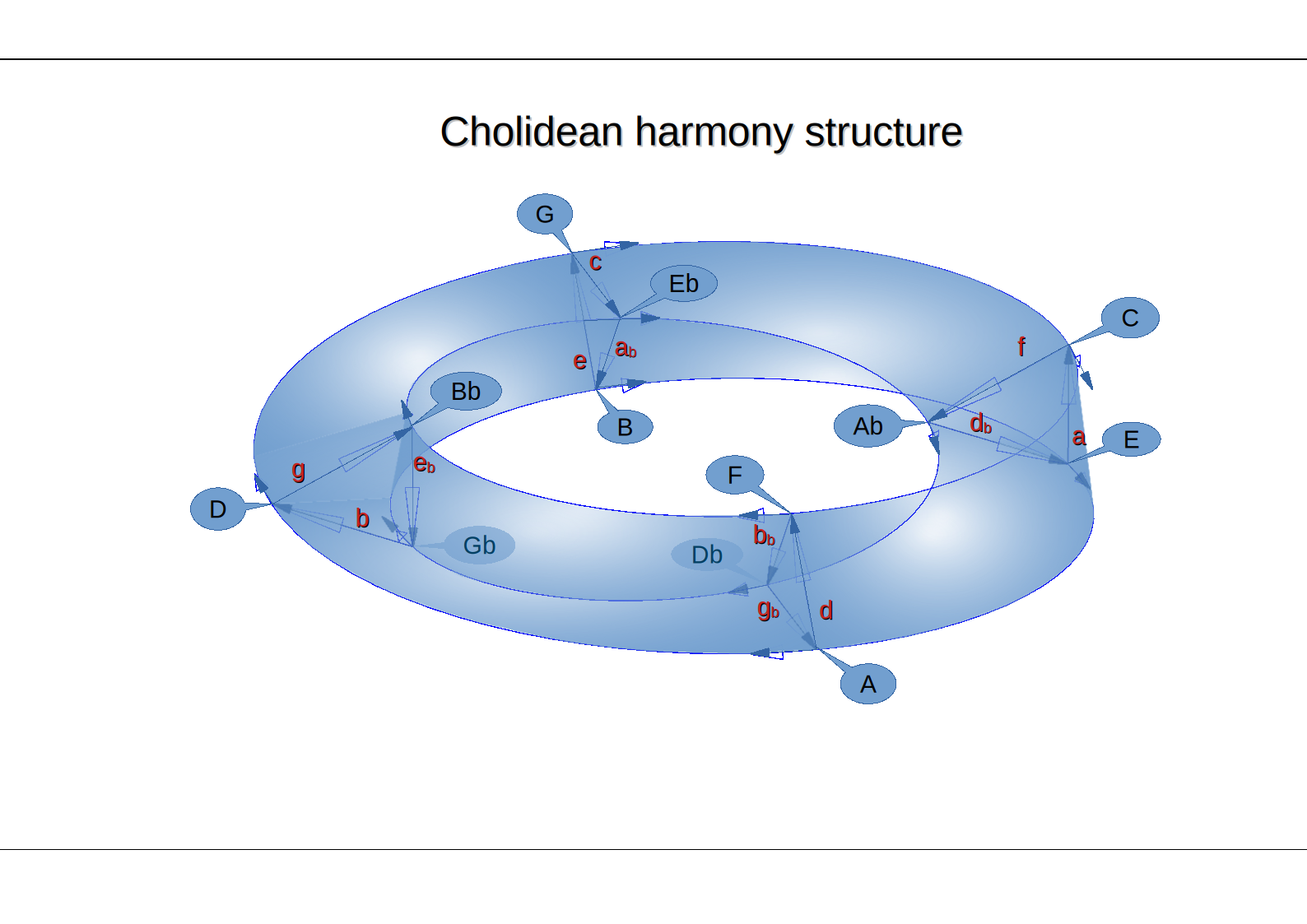
The systematic recording of thoughts on musical harmony led to the placement of the twelve musical tones on a constructible three-dimensional surface of an umbilic torus. To this visualized link of mathematics and music I gave the personal name Cholidean harmony structure.

The course of creation of the above link is recorded in pdf file. The broader background to its creation is set out at the beginning of this discussion.

Here are excerpts of the introduction and epilogue, the audio content, and the main images of the file.

License: CC BY-SA 4.0

This work is licensed under a Creative Commons “Attribution-ShareAlike 4.0 International” license.

Introduction

In an attempt, out of curiosity, to have a rudimentary understanding of musical harmony, without prior special knowledge, I read Open Music Theory, which looks similar to Integrated Musicianship: Theory, and two books by Arnold Schoenberg, THEORY OF HARMONY and Structural Functions Of Harmony. Schoenberg’s books particularly influenced my perspective.

…

My use of mathematical and physical concepts (such as fractals, category theory, group theory, dual spaces, energy, entropy, velocity, etc.) is intended as an attempt to create a system of reference, as a mnemonic rule, with as much consistency as possible to minimize exceptions to be memorized, and completeness to relate to as much material as possible from what I have read.

The present is not suitable for anyone who wants to learn harmony. There is a danger that a possibly distorted and incomplete view may be considered correct or complete. On the contrary, one already familiar with harmony can gain from a new perspective, even through demonstrating that this perspective is incorrect or incomplete.

Contents

  1. Let there be time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
  2. Tonality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
    1. Homomorphism . . . . . . . . . . . . . . . . . . . . . . . . . . 10
    2. Classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
    3. The space of tones and tonality . . . . . . . . . . . . . 12
    4. The missing tonality . . . . . . . . . . . . . . . . . . . . . . . 17
    5. Tonality as a springboard for changes . . . . . . . 21
    6. Melodies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .26
    7. Chords and scales . . . . . . . . . . . . . . . . . . . . . . . . . .28
      1. Umbilic torus . . . . . . . . . . . . . . . . . . . . . . . . . .28
      2. Minor chords . . . . . . . . . . . . . . . . . . . . . . . . . .32
      3. Relative scales . . . . . . . . . . . . . . . . . . . . . . . . .33
    8. Harmony progressions . . . . . . . . . . . . . . . . . . . . .37

Audio content

Visual content

Cholidean harmony structure

Epilogue

Although the purpose of writing the present was to systematically record, before I forgot, what I thought I had understood about musical harmonic progress, I have finally completed a wonderful, for me, mathematical journey. It is striking how, from two basic supporting branches, the minimal approximations of the frequencies of the twelve-tone system and the manifold, which is a tool used extensively in general relativity, arose the three-dimensional surface on which the twelve frequencies and twenty-four chords and scales can be placed, visualizing their basic relationships.

Even if the claims concerning the relationships between chords and scales are questioned, and indeed it would be much more useful to question them, I believe that the three-dimensional surface of the harmonic structure will remain an objective visualization tool for any musical theory on the twelve-tone system.

In the above sense, it is not necessary to read the whole article, but only the construction of the surface and the notation of the twelve tones on it. Reading this will be of interest to those who are curious as to how the manifold came about from scratch, almost on its own, and those who understand that changing the basic conditions of its creation, such as using three basic branches instead of two, would probably also bring about the need to modify it, perhaps into a three-dimensional object with more stations and/or edges of each station, than the two-dimensional surface constructed.

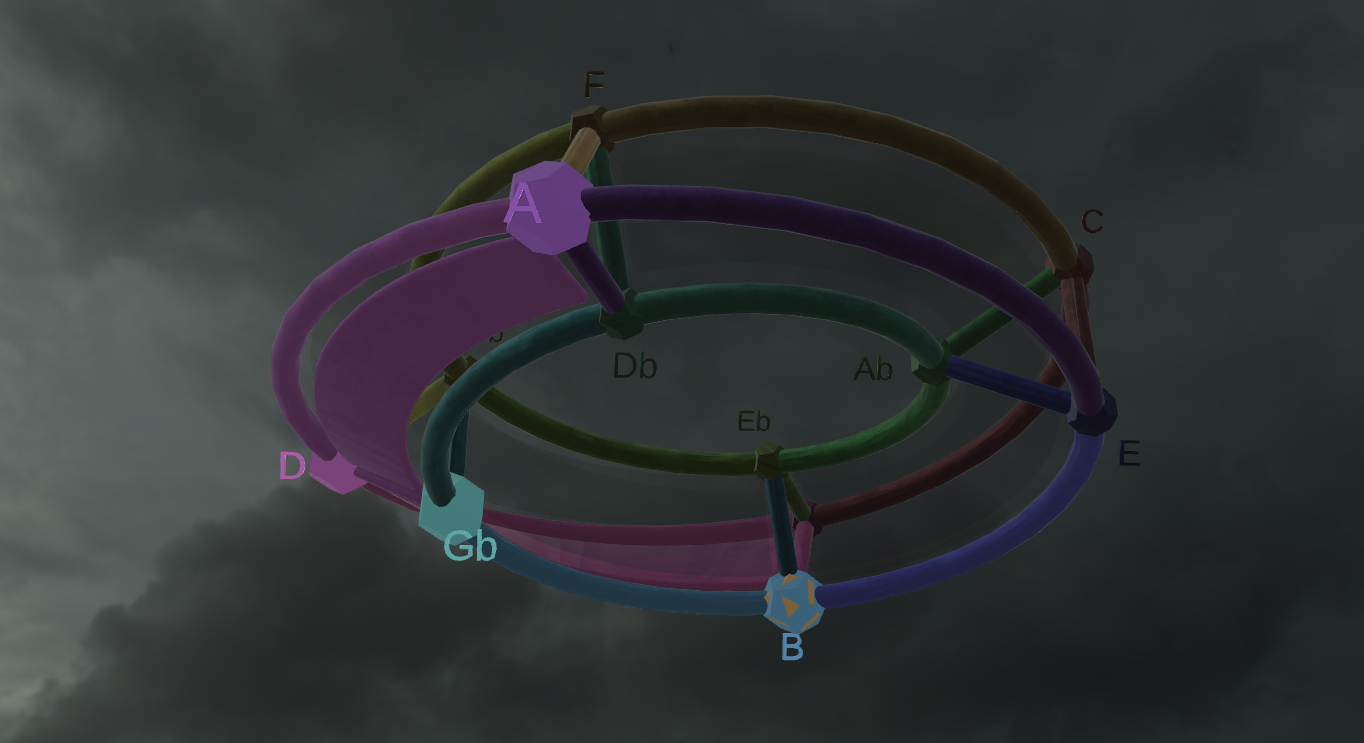
A 3D visualisation on midi files was created here Cholidean harmony structure Video screen record

This translation was possible because DeepL.com (free version) was very respectful of the LaTex pdf creation commands.

Readers’ views