Meet the musical intervals and the Neo-Riemannian moves, through an analogue clock.
After circle of fifths and diatonics, continuing to read about fundamentals of music theory, I find that the music clock can help in easily identifying the intervals of common musical terminology.
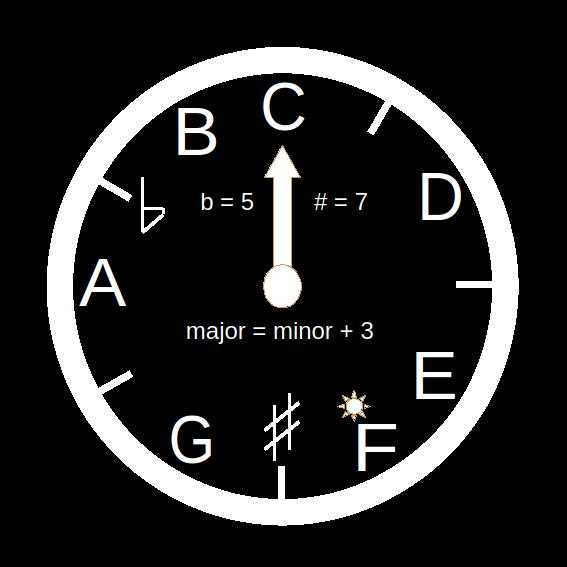
Our music clock
Terminology
A musical interval, as the difference between two pitches, can be defined in an absolute way as the number of semitones that separate them. But the total number of semitones of an octave is 12, while the notes of a scale are 7. The relation of tones in a melody is necessarily expressed as the relation between the 7 tones of the scale used. Thus, to define an interval, it is necessary to use two terms. The first noun term will indicate the relationship to the 7 tones of the scale and the second, as an adjective of the first, will specify the exact interval in number of semitones.
Size
The interval’s size expresses the relationship with the 7 notes of each scale. It is the number of notes that exist between the highest note and the lowest, including the lowest note. For this reason, it does not affect accidentals. E.g. the interval bbE-#A has the same size as E-A, which counting E(1)-F(2)-G(3)-A(4) tells us that it is a 4th.
Intervallic inversion
We have the inversion of an interval when we reverse the tones and the lowest appears as the highest and vice versa. E.g. the inversion of E-A is A-E. Since the sum of an interval and its inversion always equals one octave or 12 semitones, (E-A)+(A-E)=(E-A-E)=E-E, each interval uniquely defines its inversion, and each change (decrease or increase) of an interval uniquely defines the opposite change (increase or decrease respectively) of its inversion. Each octave is completed after 7 notes, so the sum of an interval and its inversion is always completed after 7 notes. However, in the magnitude of both the interval and its inversion we include their initial note. Thus, the nominal values of these two intervals always sum to 7+2=9. E.g. since E-A is 4th, then A-E is (9-4=) 5th.
Furthermore, the inverse of 6th is 3th, if we increase a 6th we decrease its inverse of 3th or if we increase a 2nd we decrease its inverse of 7th and so on.
Quality or type of intervals
The quality or type of each interval is named according to whether the interval itself, or its inversion, seen as a distance from the tonic of some scale, can determine the kind (minor or major) of that scale.
Since the C tone occurs, according to the musical clock, at 00:00 o’clock, it is very convenient to consider the intervals under consideration as distances from the C tonic and to compare them with the distances of C major tones. Let us consider the intervals from the tonic of C major (00:00 o’clock) and the intervals from the tonic of A minor (09:00 o’clock).
| size | (unison) 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | (octave) 8th |
|---|---|---|---|---|---|---|---|---|
| major scale | ||||||||
| Interval from C (00:00) | 0 | 2 | 4 | 5 | 7 | 9 | 11 | 12 |
| minor scale | ||||||||
| Interval from A (09:00) | 0 | 2 | 3 | 5 | 7 | 8 | 10 | 12 |
We find that the 3rd, 6th and 7th intervals, because they differ between the major and minor scales, are immediately distinguishable, as distances from their tonic. For this:
The intervals of 4, 9 and 11 semitones are called 3rd major, 6th major and 7th major respectively. The intervals of 3, 8 and 10 semitones, which are 1 semitone shorter, are called 3rd minor, 6th minor and 7th minor respectively.
The 2 semitone interval from the tonic, because it is common to both scales, raises doubts as to its name. To name it consistently, we must resort to the 3rd and 6th or whatever happens in the union of each interval with its inversion.
As mentioned above, this compound always gives a distance of 12 semitones. Let us imagine an imaginary distance of 3½ semitones. Its inverse will equal 8½ semitones.
If we increase the first by ½ a semiton, to keep the sum 12, the second distance is reduced by ½ a semiton. The first becomes 4 semitones, i.e. 3rd major, and the second becomes 8 semitones, i.e. 6th minor. So, the sum of the 3rd major and 6th minor is also 12. If we decrease the first by ½ a semitone to keep the sum 12, the second distance increases by ½ a semitone. The first becomes 3 semitones, i.e. 3rd minor, and the second becomes 9 semitones, i.e. 6th minor. So, the sum of the 3rd minor and 6th major equals 12.
Consistency requires that each major interval together with its minor inversion gives an interval of 12 semitones.
With the help of the above observation, the unknown 2nd of the 2-semiton interval can be determined. Its inversion equals 10 semitones, which have already been characterized as the 7th minor. In order to complete the 12 semitones, the 7th minor must be joined by a 2nd major. Consequently, the interval of 2 semitones is called the 2nd major, although it is common to both types of scales.
The 4th, of 5 semitones, is a common interval in both scales. However, its inverse, the 5th, of 7 semitones, is also a common interval on both scales. Because of the above, one cannot decide whether these intervals, the 4th and 5th, from the tonic, are created by major or minor scales. So, two different classes cannot be defined for these intervals, but only one, that of the perfect interval, since both scales produce the same distances. The same is true for the 1st (unison) and 8th (octave) intervals.
Because of the above, the 1st, 8th, 4th and 5th intervals are called perfect intervals.
Augmented and Diminished Qualities
We have defined the minor intervals so that increasing them by 1 semitone gives the major intervals. Further increasing the major intervals by 1, 2, 3, and so on, simply produces the single, double, triple, and so on augmented intervals.
We have defined the major intervals so that decreasing them by 1 semitone gives the minor intervals. Further reduction of the minor intervals by 1, 2, 3, and so on, simply produces the single, double, triple, and so on diminished intervals.
In perfect intervals there is no differentiation. Increasing perfect intervals produces, directly, augmented intervals, while decreasing perfect intervals produces, directly, diminished intervals, just as in other major or minor intervals.
Recognition of intervals
The recognition of intervals is easy if they are compared, with the help of the musical clock, with the distances from the tonic of the C major.
We need of course to have memorized, apart from the obvious 1st and 8th, that both the 4th, of 5 semitones (b=5), and the 5th, of 7 semitones (#=7), are perfect intervals. It is not difficult, however, since the 5th and its 7 semitones (#=7) are known to play a dominant role in music theory. Despite the fact that it is well known that (b + # = 12), the associated 4th and 5th symbols of flat (b) and sharp (#) are noted, anyway, as a reminder on the musical clock.
The identification procedure is as follows:
- We identify from the names of the tones (ignoring the accidentals) the size of the interval.
- We determine the number of semitones of that interval on the major scale (hour difference from C of 00:00). Let’s call it the reference interval.
- Given the accidentals, we find the difference in hours (semitones) of the highest tone from the lowest tone.
- If the difference is equal to that of the reference interval, then we have a major interval or perfect interval. If the difference is other than that of the reference interval, then we vary the quality of the major or perfect interval so that the compared intervals are equal.
Examples
-
F-C: F-G-A-B-C 5 tones, this is the 5th, which on the major scale is perfect and lasts 7 hours. The duration of this interval equals C(12)-F(5)=7, the same as the reference interval. No variation is needed, the F-C interval is perfect 5th, P5.
-
bE-bC: E-F-G-A-B-C 6 tones, this is 6th, which on the major scale is major and lasts 9 hours. The duration of this interval equals bC(11)-bE(3)=8 hours (semitones). The major must be reduced by 1, therefore, the interval bE-bC is minor 6th, mi6.
-
bG-E: G-A-B-C-D-E 6 tones, this is the 6th, which on the major scale is a major and lasts 9 hours. The duration of this interval is equal to E(16)-bG(6)=10 hours (semitones) (From 6 to 4 is 10 hours). The major must be increased by 1, therefore, the bG-E interval is augmented 6th, A6.
-
G-bbE: G-A-B-C-D-E 6 tones, this is the 6th, which on the major scale is major and lasts 9 hours. The duration of this interval equals bbE(14)-G(7)=7 hours (semitones) (From 7 to 2 is 7 hours). The major must be reduced by 2, therefore, not once in a minor but once more in a diminished. The interval G-bbE is diminished 6th, d6.
-
A-C-C: A-B-C-…-C 10 tones, this is the 10th (7+3=10), which in the major scale, like the simple 3rd, is a major and lasts 4+12=16 hours. Instead of the comppund interval of 16 hours, we will refer to the equivalent simple interval of the 3rd of 4 hours. The duration of this interval, in its simple form and ignoring the extra octave, equals C(12)-A(9)=3 hours (semitones). The major of 4 hours must be reduced by 1. Therefore, the interval A-C-C is minor 10th, mi10.
-
bbE-bA: E-F-G-A 4 tones, this is 4th, which in the major scale is perfect and lasts 5 hours. The duration of this interval is equal to bA(8)-bbE(2)=6 hours (semitones). The major needs to be increased by 1. Therefore, the interval bbE-bA is augmented 4th, A4.
Personally, I have the impression that the writing of the present has been a double benefit for me. The first is that, even if I forget the details, I can easily recreate them from memory, with the help of the musical clock. The second is the understanding that the current terminology contains more information than the number of semitones that make up a musical interval. For example, for the interval bbE-bA, not only are the 6 semitones of its span mentioned, but, by stating it as an augmented 4th and not a deminished 5th, additional information is provided about its connection to the rest of the structure of whatever composition uses it.
Neo-Riemannian moves
The following relates to my understanding of the chapter on movements on three-voice Neo-Riemannian chords.
Neo-Riemannian moves involve the smoothest transitions from a consonant chord to a consonant chord of opposite quality (from major to minor or from minor to major). Therefore, chords with a diminished 5th, such as B-D-F, are not enclosed, but B-D-#F is enclosed instead.
The fact that the concept of tonality is not used, makes the use of the musical clock natural. Each chord is symbolized by the time it occurs followed by the symbol ‘M’ if it is major, or ’m’ if it is minor. E.g. 9M=A-C-E or 11M=B-#D-#F.
The moves
Tonnetz
The basic movements, which refer to the movement of only one voice and to the Tonnetz diagram, are denoted by the symbols ‘R’, ‘L’ and ‘P’.
- P The chord moves to the opposite chord of the same time. E.g. (C-E-G) 0M-[P]-0m (C-bE-G).
- Major chords (with 4-3 semitone intervals) can move to the opposite chords either 3 hours earlier (R movement) or 4 hours later (L movement). e.g. (C-E-G) 0M-[R]-9m (A-C-E) or (C-E-G) 0M-[L]-4m (E-G-B)
- Minor chords (with 3-4 semitone intervals) can move to chords of opposite quality either 4 hours earlier (L movement) or 3 hours later (R movement). e.g. (C-E-G) 0m-[L]-8M (bA-C-bE) or (C-E-G) 0m-[R]-3M (bE-G-bB).
An other easy way is to memorize that root of Major chords can move to a root a Major third higher (or a minor third lower) and root of minor chords can move to a root a minor third higher (or a Major third lower).
The Tonnetz diagram graphically describes the above movements.
Cube dance
The R movement is the only one that moves one voice by a tone instead of a semitone. If, in the direction of R, we introduce the semitone motion, we end up with an augmented chord in between. I denote augmented chords by the pitch times of the voices, e.g. [0:4:8] = C-E-#G. The intermediate chord is of the same time as the major of the R movement and 3 hours later than the minor. An advantage is gained by the fact that the augmented chord is perfectly symmetrical, so that, in addition to the R destination, the ending can be made in the other two notes corresponding to the other voices of the augmented chord.
For example, the movement (C-E-G) 0M-[R]-9m (A-C-E) is developed as (C-E-G) 0M - [0:4:8] (C-E-#G) - 9m (A-C-E), which is the ending 3 hours earlier than 0. But it can, just as smoothly, end in a minor 3 hours earlier than 8 (time belonging to the incremental [0:4:8]). Thus, to have the new movement (C-E-G) 0M - [4:8:0] (E-bA-C) - 1M (bD-F-bA).
Personal notes on the above mentioned chapter, in English, can be found in pdf.
Postscript
Extensive use of the musical clock, referred to as ‘clock face’, appears in the chapter VIII 20th and 21st century techniques of the very good online music theory book “OPEN MUSIC THEORY”. But, because the aforementioned chapter is about methodologies for music analysis through mathematical set theory (don’t be alarmed! as you know clocks, you know sets too), the musical clock is used as a descriptive tool for analyzing ‘atonal’ music, with no reference to tonalities, hence no reference to the key signatures, where we mostly used it.
(Important reference: A few months after writing this, I came across the amazing, in every respect, website Integrated Music Theory of which I could not fail to mention it).