Circle of fifths in music, through an analog clock
In my youth I studied classical guitar. I read a lot of sheet music and knew how to use key signatures. But I’ve never been able to identify, at a glance, the major or minor scale pair that defines a, non-trivial, signature. I thought this ability belonged only to very experienced musicians. A few days ago, I realized that I was completely wrong. Identifying the pair of scales that defines a key signature is as easy as using a wristwatch.
Even if you have no experience in music theory, you do not need to memorize the following circle of fifths to recognize from the the key signature the major and minor scales involved. Just by looking at the signature, ask yourself “what time does it say?”
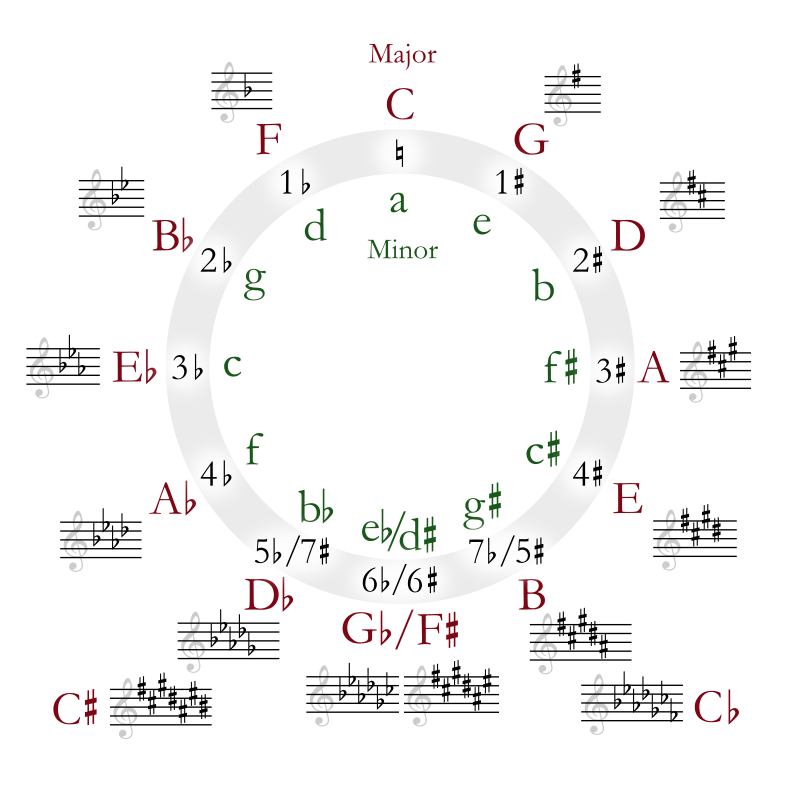
The Circle of Fifths
Regular time as isomorphism of music note
We are all familiar with the division of time into hours and the use of analogue clocks, which groups hours into twelve-hour periods.
Math hobbyists easily recognize on a clock the modular arithmetic with a divisor of 12. They also recognize that the repetition of the octave refers directly to the aforementioned modular arithmetic.
Musicians know that an octave is divided into twelve equal semitones, just as the twelve hours of a clock is divided into twelve equal hours. If they are even a little bit into mathematics, I think they will find it elementary that normal time, divided into hours, is isomorphic to music, divided into semitones, as long as addition and multiplication between hours defines addition and multiplication between semitones.
The music clock
We are all familiar with the use of analogue clocks that group hours into twelve-hour periods. Because of the use of clocks, we are already familiar with the modular arithmetic on divisions of 12. So, even if we know nothing about music, because of the isomorphism between time, divided into hours, and music, divided into semitones, we are already familiar with division of music into groups of 12 semitones. So, everyone is familiar with the division of music into octaves and that is, because each octave consists of exactly 12 semitones. And what is amazing is that the same wristwatch, we use to measure the hours of time, can be used to measure the semitones of music, provided we change the symbols on it.
For ease of understanding, we consider each musical note or scale as an event that occurs at a particular time. By defining that the note C, or scale C major, always occurs at 00:00, we construct the background of the clock, which eventually represents an octave.
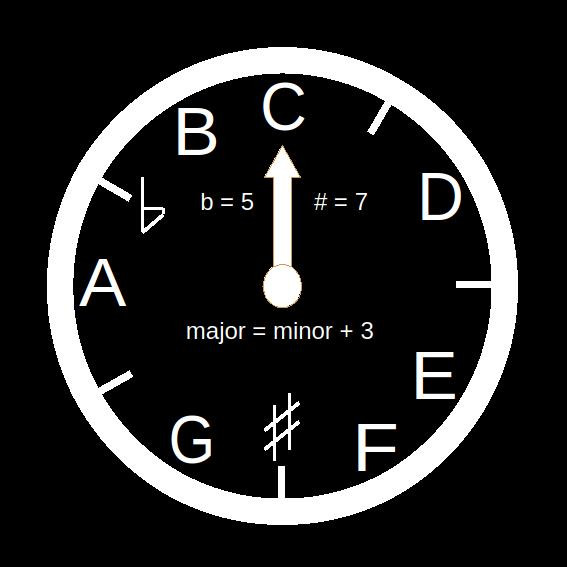
Our music clock
- The notes C, D and E are marked at the small even hours 0, 2 and 4 o’clock respectively. The remaining notes F, G, A and B are marked at odd hours 5, 7, 9 and 11 respectively.
- The small lines indicate the black keys of the piano. E.g. at the 3rd hour either D# or Eb occurs.
Basic relations
to help understand the circle of fifths.
- Every twelve hours the clock shows the same time. This means that when we want to calculate the time that the clock will show after any interval, the intervals 0, 12, 24, 36, 48 etc. can be ignored. E.g. if it is now 00:00, after 49 hours the clock will show (49-48=1) 1 hour.
- Suppose someone moved the clock hand from 00:00 to 05:00. There is no way to tell whether the hand was moved 5 hours forward (clockwise) or 7 hours back (-7) (counterclockwise). This is because, for the modular arithmetic of the clock, any counterclockwise movement of the hand by a (denoted by -a) is equivalent to a clockwise movement by 12-a.
- Each clockwise step in the circle of fifths is a transfer of the scale one fifth higher. That is, it is always a transfer 7 semitones higher. On our clock, it is always a transfer to the scale that occurs 7 hours later. The key signature of the new scale differs from the signature of the previous scale only in that a sharp (#) is added. For this reason, the hand, of our clock, shows the C major, which occurs at 00:00 and has an empty signature. Thus, the number of accidentals in a major scale signature, gives us the “time” difference between it and the C major. In view of the above, it turns out to be very useful to assign, in addition, to the symbol # the value 7, (#=7, in the sense of each step’s “7-hour movement forward”).
- Each counterclockwise step in the circle of fifths is a transfer of the scale one fifth lower. By our clock, it is always a transfer to the scale that occurs 7 hours earlier. As we have already seen, 7 hours back is equivalent to 5 hours forward. The key signature of the new scale differs from the signature of the previous one only in that a flat (b) is added. In view of the above, it turns out to be very useful to assign, in addition, to the symbol b the value 5, (b=5, in the sense of each step’s “moving 7 hours backwards”).
Conclude the minimal operations required to explain the equivalence of signatures observed in the cases of the three scales at the bottom of the circle of fifths image.
- If we move a times by 12 semitones, i.e. one octave at a time, the clock hand is not affected. Nor, of course, if we move 5 times 12 semitones at a time. So, we can write a*12=5*12 (mod 12) => a*(7+5)=12*5 => a*7 = 12*5-a*5 => a# = (12-a)b. So, we see that the signature consisting of a sharps is equivalent to the signature consisting of 12-a flats.
- In the same way, we can write a*12=7*12 (mod 12) => a*(5+7)=12*7 => a*5 = 12*7-a*7 => ab = (12-a)#. So, we see that the signature consisting of a flats is equivalent to the signature consisting of 12-a sharps.
In theory, we could see signatures up to 11 sharps or flats. (The 12 accidentals would mean moving by 12*7 or 12*5 semitones, i.e. by 7 or 5 octaves, so we would be back in C major again.) But, always preferring the signatures with the fewest accidentals, we would not expect to find signatures with more than 6. E.g. instead of seeing a signature of 10 sharps, we will find it as a signature of (12-10=) 2 flats.
Signature recognition (what time does it say?)
The music clock shows us that it is 00:00 o’clock. That means we are in the C major scale. Each sharp means the major scale after 7 hours (# = 7). That is, a signature of a sharps means the major scale a*7 hours after 12.
(If our clock showed 9 o’clock, i.e. A minor, then a sharps would mean the minor scale a*7 hours after 9. But we would have difficulty in constructing the signatures, as we will see below. So, with the pointer at 12, we always find the time of some major scale. The twin minor scale, which has the same signature, just happens 3 hours earlier.)
Each flat means the major scale after 5 hours (b = 5). That is, a signature of a flats means the major scale a*5 hours after 12.
To identify the major scale of any signature, we only have to answer as to what time it will be after a certain period of time, determined by the type and number of accidentals of the signature.
Examples assuming that the time is 00:00.
- Signature with 3 sharps: 3#=3*7=21. What time will it be after 21 hours? We all know that, at 21:00, it is 9 o’clock. Our clock at 9 o’clock shows A. So, 3 sharps have the A major scale. Instead of 9, the minor occurs 3 hours earlier. So, at 6 o’clock. Since we see sharps and the basic tone will read in score as F#, the scale must have the same name. Thus, we’ll express 6 o’clock minor scale as F#. So, 3 sharps has also the signature of F# minor scale.
- Signature with 4 flats: 4b=4*5=20. What time will it be after 20 hours? We all know that, at 20:00, it is 8 o’clock. Since we see flats, we’ll express 8 o’clock by flat. Our clock at 8 o’clock shows Ab. So, 4 flats have the Ab major scale. Instead of 8, the minor occurs 3 hours earlier. So, at 5 o’clock. F. So, 4 flats has also the F minor scale.
- Signature with 9 sharps (outside theory): 9*7=63. What time will it be after 63 hours? 63=5*12+3=3 (mod 12). It will be 3 o’clock. Since we see sharps, we’ll express the 3rd hour by sharp. D#. So, 9 sharps has the D# major scale. Instead of 3, the minor occurs 3 hours earlier. So, at 00:00 o’clock. C. Therefore, 9 sharps have also the C minor scale.
-
- But instead of 9 sharps, it is much more economical to express the same signature with 3 flats (3=12-9). With 3 flats we have 3*5=15. We all know that at 15:00 it is 3 o’clock. What we have already found. But since we have flats, instead of D# major, let’s consider that we have Eb major. As well as the C minor, of course, 3 hours earlier.
From the signature alone, no distinction can be drawn between the major and minor scales concerned. Only the distinction of the basic tone, through the score, can provide this additional information. (If we know the tonality, relative to our clock, we can assume that the fourth chord occurs after b hours [b=5], while after # hours [#=7] the fifth chord occurs.)
Construction of signature
From the way a signature is identified, it is clear that the corresponding scale will occur either after hours multiples of 5 (if the signature uses flats) or after hours multiples of 7 (if the signature uses sharps). Except in the trivial case of the scales at 5 and 7 o’clock, it will never take more than two easy trials to find the time interval that will give us the type and number of accidentals.
Minor scale signature construction
We transform the problem and construct the key of the twin major scale that occurs three hours later. E.g.
- We want the signature of the B minor. B occurs at 11 o’clock. So, we will construct the signature of the 3 hours later major scale. 3 hours after 11 o’clock will be 2 o’clock. So, we will construct the signature of the 2 o’clock major. In this case, the D major.
- We need F minor’s signature. The F happens at 5 o’clock. So, we will construct the signature of the 3 hours later major scale. 3 hours after 5 o’clock, it will be 8 o’clock. So, we will construct the signature of the 8th hour major. (We will not name it explicitly yet because, for the moment, we do not know which name of G-sharp or La flat is more correct.)
Major scale signature construction
The placement of sharps or flats is done after finding the type and number of accidentals. When we see e.g. 3#, with the operation 3*7=21 we already know that 21 is a multiple of 7, that 7 corresponds to a sharp and that the clock shows 9 o’clock, in A.
But we ask for the reverse, looking for the smallest possible multiple of either 7 or 5. If we knew 21, we would conclude that it is a multiple of 7, hence the accidentals are sharps, and dividing 21 by 7 would give us 21/7=3, i.e. the number of sharps in the signature.
But we only know that we want the signature of the A major and that the Α happens at 9 o’clock. 9 is not a multiple of either 7 or 5. But we are not at a dead end. If we add a twelve-hour period to 9 o’clock, at 9+12=21, the clock hand will continue to show A. 21 is easily recognized as a multiple of 7 and so the problem is solved and we place the 21/7=3 sharps (#=7).
So, the procedure is as follows:
We ask for the signature corresponding to time a.
- If a=5 (i.e. we ask for the F major), because b=5, we place the first and only flat at 10 o’clock. (The flat symbol at the 10 position on the clock exists to remind us that the first flat is placed as B flat).
- If a=7 (i.e. we ask for the G major), because #=7, we place the first and only sharp at 6 o’clock. (The sharp symbol at the 6 o’clock position is there to remind us that the first sharp is placed as F#).
- Otherwise, consider a+12. If it is a multiple of either 5 or 7, place the appropriate flats or sharps respectively. If a+12 is not such a multiple, then we add another twelve hour interval, which, a+24, will certainly be such a multiple, which will indicate the type and number of accidentals of the signature we seek.
(For the interval of 35 hours, I suggest the 5 sharps of the B major as less than the equivalent of 7 flats of the C flat major.)
Placement of accidentals
- Sharps: The first sharp is placed at 6 o’clock (F#). Since #=7, each subsequent sharp is placed 7 hours after the current one. Thus, by following the hands of our musical clock, the sharps are placed in order at hours 6, 1, 8, 3, 10, 5, 12, etc. That is, we have in order F#, C#, G#, D#, A#, E#, B#etc.
- Flats: The first flat is placed at 10 o’clock (Bb). Since b=5, each subsequent flat is placed 5 hours after the current one. Thus, by following the hands of our musical clock, the flats are placed in order at hours 10, 3, 8, 1, 6, 11, 4, etc. That is, we have in order Bb, Eb, Ab, Db, Gb, Cb, Fb, etc.
- Natural tones: The tones that remain unchanged are those that correspond to the placement of the tones of the opposite category.
Examples
-
3 o’clock major: 3+12=15. Multiple of 5, so flats and the scale, expressed in flat, is E flat major. The number of flats is 15/5=3, so 3 flats. The 10, 3 and 8 o’clock. (That is 11-1, 4-1 and 9-1.) That is, Bb, Eb and Ab.
-
4 o’clock major: 4+12=16 inappropriate. 16+12=28. Multiple of 7, so sharps and the scale is E major. Number of sharps 28/7=4, so 4 sharps. 6, 1, 8 and 3. (That is 5+1, 0+1, 7+1 and 2+1.) That is, F#, C#, G# and D#.
-
1 hour of major: In essence we wish to drive to the region of Neapolitan chord (1 hour of major). 1+12+12=25. 25/5=5 so 5 flats. That is, we desire access to the (bD) major scale. Since the tones of each scale are 7, the invariant tones are 7-5=2. Therefore, the natural common, with the C major where we are, tones are those corresponding to the placement of 2 sharps, i.e., F and C (on which we would place the first 2 sharps).
In order not to commit ourselves to the C major, we identify these 2 tones as those corresponding to the 4th and 1st degrees of the major scale. These belong at the same time only to the (IV) chord of the major scale, but in Neapolitan by necessity we will use the alteration of bA which makes it a minor (iv). It seems then that a short smooth way to get to Neapolitan is through the minor scale which corresponds to the 4th degree of the major scale where we are. (A progress like I-iv-VI/iv, because Neapolitan is the (VI) major of iv minor scale.)
The simplest signature
In trying to study the basics of harmony, I often faced the question “what is the scale with the simplest signature that contains a particular accidental?”
-
If the alteration is a flat (b), since the first flat (bB=10th hour) corresponds to F major (5th hour), then the simplest major scale occurs 5 hours before the flat. E.g. the simplest signature containing the bE (3rd hour) corresponds to the 10th hour major (bB major) - or 7th hour minor (g minor).
-
If the alteration is a sharp (#), since the first sharp (#F=6th hour) corresponds to the G major (7th hour), then the simplest major scale occurs 1 hour after the sharp. E.g. the simplest signature containing the #D (3rd hour) corresponds to the 4th hour major (E major) - or 1st hour minor (#C minor).
The above answer is almost equivalent to the observation that a signature with sharps corresponds to a major scale 1 hour after the sharp and a signature with flats corresponds to the major scale occurring at the second to last flat.
Conclusion
It was immensely amusing when I understood that, despite my impression to the contrary, I finally knew all the key signatures of the circle of fifths. But it was also a little embarrassing that it took me half a century to realize it. If only I had, earlier, my music clock.
To those who will “own” the music clock, I wish them the best use of it.
Postscript
Extensive use of the musical clock, referred to as ‘clock face’, appears in the chapter VIII 20th and 21st century techniques of the very good online music theory book “OPEN MUSIC THEORY”. But, because the aforementioned chapter is about methodologies for music analysis through mathematical set theory (don’t be alarmed! as you know clocks, you know sets too), the musical clock is used as a descriptive tool for analyzing ‘atonal’ music, with no reference to tonalities, hence no reference to the key signatures, where we used it.
(Important reference: A few months after writing this, I came across the amazing, in every respect, website Integrated Music Theory of which I could not fail to mention it).