Chess: Consistency of beliefs in transpositions
Strategy against the game.
For too long I was playing games against the game itself. That is, I believed that, objectively and regardless of the opponent, there is an optimal strategy by which victory is achieved. The point, whether in a study or in a match, was to find that strategy. This view created great pressure to find an optimal move and, at the same time, undue frustration when any positional advantage could not be realized.
When a supercomputer solves the game, each position can be assigned to the numbers {-1, 0, 1} depending on the outcome of the optimal play of both sides. Then there will be an objective evaluation even of the initial position.
When we play against the game, we implicitly admit that there is a winning side and seek its strategy, in which only moves are chosen that result in positions with an objective evaluation of the sign of victory. But even if there is an objective evaluation leading to a winning strategy, by looking for it, we easily fail to recognize that the non-winning side, by necessity, bases its optimal strategy on a subjective evaluation of the position.
The losing side, if it knows its human opponent, must choose positions where the probability of a mistake by him is increased. If he does not know him, he must choose positions where the probability of a mistake by him is reduced. Usually he must do so at the same time, choosing positions where the probability of a greater error by the opponent than by himself is increased. Consequently, the losing side, in any given position, depends for its optimal moves on the opponent it faces and on its own ephemeral or permanent weaknesses.
Subjective positional evaluation
Optimal choice axiom
We accept that, after each player has chosen which colour to play with, each game proceeds with optimal move choices by both opponents.
The above axiom is self-evident for any rational analysis. But it filters out of analysis any game containing non-rational moves. For example, if an unknown opponent starts with 1.)e4 and we believe that the answer 1)…e5 is stronger than 1)…c5 then, by the axiom of optimal choice, we ought to answer 1)…e5. Cases such as choosing 1)…. c5 as the answer because we are simply bored of answering with 1)… e5 are outside the rational framework and, therefore, are not the subject of this article.
Assumption of a tie result
Watching the play of the most powerful chess programs, we can relatively easily adopt the assumption that, with optimal strategy of black against optimal strategy of white, the result of each game is a draw.
Any position resulting from optimal play is objectively assessed as a draw. Thus, if we achieve optimal play, any victory depends entirely on the opponent’s mistakes, while our defeat, if the opponent plays optimally, depends entirely on our own mistakes.
How many and which mistakes each player will make does not depend objectively on the rules of the game. Therefore, the existence of mistakes depends on the opponents, so any assessment of the number of mistakes that will be made can only be subjective.
To further understand the notion of the subjectivity of evaluation, which depends on both us and the opponent, suppose that, when playing with white against an equal opponent, the evaluation of the initial position is expressed by the fact that “white has the initiative”. When we play against the world champion, the evaluation of the same initial position is expressed by “black wins”.
The evaluation of the moves that we observe in the analysis of the chess machines is also subjective. It is an evaluation based on their opponent and, in this case, they evaluate considering that they are playing against themselves. In other words, what human players do in their analysis, except that chess machines are many times more powerful than humans.
The objective evaluation of each position comes from optimal play and cannot be useful in chess games, because each such position, of optimal play, is consistently evaluated as a draw. The only useful evaluation of each position in chess games is any subjective evaluation that estimates the probability of existence of mistakes by the players, thus it does not depend on the rules of the game.
In conclusion, the useful evaluation for chess games is subjective and assesses the errors that may occur in the rest of the game.
The game of chess today has two dimensions. The dimension of the search for objectively optimal moves, through the chess theory that is developed on this, and the competitive dimension. The latter is based on the human errors of the opponents and the subjective evaluations during the games. When the end of the game as a chess theory is signalled, that is, when the game is fully resolved by future supercomputers, then chess will henceforth be a pure competition, like most other sports, where human opponents will compete in the virtues that the nature of chess demands.
Fun assumption of equality of initial moves
The tie assumption is enough to demonstrate the usefulness of subjective evaluation in itself. But it seems amusing to additionally adopt the view that it is preferable to play any initial white move than to choose black.
Due to the assumption of a tie, the best result that White can achieve against Black’s optimal answers is a draw.
For a player to choose black is equivalent to the rules allowing white not to start with any of the 20 initial moves, i.e. with any of the pair of allowed moves of each pawn or knight, but to grant the privilege of the first move to black. We have already accepted, however, that this is the worst initial choice a player can make. Consequently, after the worst choice of black suit, the result is again a draw.
Since White’s best result is a draw and his worst, granting the privilege of the first move, is still a draw, then each of his 20 initial moves is objectively evaluated as a draw. So all of White’s 20 initial moves are objectively equal.
The fun of the thing, referring to the preceding, is that one cannot accept a) that it is better to play any white move than to choose black, b) that black can achieve a draw and, at the same time, claim c) that the move e.g. 1)e4 is objectively better than starting with 1)h3. 1)e4 can be better than 1)h3 only subjectively, because e.g. the opponent is human and is expected to make more mistakes by facing 1)e4 than 1)h3.
Properties of subjective evaluation
Notations
Let us consider the evaluation as a function of the possible chess positions on the natural numbers. It does not matter which natural numbers the positions are assigned to. What matters is that the comparison of positions corresponds to a comparison of numbers. So let us express the evaluation of the positions of full equality by the number $0$. Positions where, thereafter, more and/or larger errors are expected from the opponent than from us, will have a positive evaluation. In the opposite case, where we, and not an opponent, are expected to make more and/or bigger mistakes, the evaluation will be negative.
Let us denote, for the sake of economy of notation, by $X$ both the position that arises after the move $X$ and its evaluation. (I think it will be clear from the context which of the two notations is in effect.) Then by $Xa$ we denote both the position that arises after the $a$ response to the move $X$ and its evaluation. $a$, in this notation may or may not be an optimal response to $X$. If $a$ is an optimal response to $X$ motion, then let us denote the resulting position, or evaluation of the resulting position, by $a^X$, setting the exponent to the position over which the base move $a$ is optimal.
Since the subjective evaluation estimates the errors that will occur during the game, and these errors are found by comparing them to the optimal play, by necessity, the evaluation of positions derived from sequences of optimal moves does not change but remains constant.
Thus, when we have optimal continuations after the $X$ move, it will hold, as far as the evaluations are concerned,
$$ X = a^{X} = Y^{a^X} = b^{Y^{a^X}} = Z^{b^{Y^{a^X}}} = ... $$
where, in the above, the moves $X, a, Y, b, Z$ were played in order, with all but the undecided first $X$ being optimal moves.
It may prove useful to define a block of a move $X$, such as $ { XaY}$ or $ { XaYbZ}$, keeping the same notation $X$, as a sequence of optimal moves after which it is the next player’s turn to respond. It is understood that the evaluation remains the same either after move $X$ or after blocks of move $X$. Despite the confusion due to the use of the same notation for the position, move, move block or its evaluation, it should be clear that for block evaluations hold
$$ X = \{ XaY \}=Y^{a^X}=\{ XaYbZ \}= Z^{b^{Y^{a^X}}} $$
Because the move block uses optimal moves it is understood that it depends on the position in which it is presented. The same sequence of moves can be a block at one position and not at another, simply because the members of the sequence are not optimal moves at the new position.
The stability of the evaluation of a long block of optimal moves is not absolute. It is only approximately true, as we will see in the subsequent section.
Accumulation of errors
The, necessarily subjective as mentioned above, evaluation of the position estimates the mistakes that will be made in the rest of the game. Suppose $a$ is our move to which the opponent responds with $Y$. If $Y$ is optimal then the evaluation, from $a$, will remain constant and hold $ a = aY = Y^a$. But if it is not optimal, the opponent has made a mistake so the rating will be increased and will hold $ a < aY $. If we continue with optimal $b$ the evaluation will not change, so it will be $ a < aY = aYb = b^{aY}$. If the opponent counters with a non-optimal move $Z$, making a mistake again, the rating will increase even more and the following will apply $ a < aY = aYb < aYbZ$.
So we see that against optimal play, the opponent’s (or our) mistakes tend to accumulate. But what exactly does optimal play against the opponent’s mistakes mean? It means that the opponent’s error that increased the evaluation precedes the error, and that then the optimal response to that error simply maintains the subjective evaluation at the elevated level it found and does not increase it.
For example, suppose that the opponent with the move $Y$ abandoned a vertical or created an weak square, etc. and for this reason he raised the evaluation. To secure the increased evaluation, we must play optimal move $b$, thereby conquering the vertical or the weak square, etc., otherwise, if we play incorrectly, the increased evaluation will be reduced. If the opponent with his mistake had not increased the evaluation, we would not have the opportunity to conquer the vertical or weak square, etc., and thus we would not improve our position.
The increase in evaluation precedes the improvement of positions.
Therefore, with optimal play, the advantages gained are accumulated, just as it was considered by Steinitz, but this only happens if the opponent’s mistakes accumulate, increasing the evaluation. In this sense, it is not the gaining of strategic advantages, such as the possession of a vertical or weak square, that is the precondition of optimal play, but optimal play, against the opponent’s mistakes, is the precondition of gaining strategic advantages.
Strategic finesse does not lie in gaining strategic advantages but in detecting an increase in evaluation, due to the opponent’s mistakes, and adapting to it with optimal play. E.g. first we detect an increase in evaluation due to abandoning a vertical and then our optimal play is likely to lead to its conquest.
This perspective seems to have an impact on the way we perceive strategy. Many times, during the game and at times when choosing openings or variations, it seems that we have to choose between several optimal moves. Each of these optimal moves probably leads the game in a different direction. This gives the illusion that we can work out long term plans and direct the game according to a general plan that we have in mind. However, whatever plan or master plan we choose is based on the opponent’s optimal responses. Thus, from a tied position, following a general plan will result in a draw if the opponent chooses between optimal moves. Despite choosing an optimal plan, there is no way to win the game against optimal play.
But if the opponent, in some move, increases the evaluation by committing a mistake, then we must be psychologically ready to abandon our plan, adapt to the new increased evaluation and direct where the opponent’s mistake forces us. If we insist on following our no-longer relevant plan, we may not only fail to win the game, we may lose it.
It is good to know where we are by following optimal plans but we have to abandon them as many times as the opponent’s mistakes. So when we are facing a weak opponent who is constantly making mistakes, we cannot follow long-term plans and at the same time claim that we are playing optimally. It is better after every move of the opponent, especially when it is unexpected and therefore suboptimal and therefore wrong, to recreate new plans from the scratch.
Instead of spending playing time thinking in depth, i.e. one choice of a sequence of moves, of which ours, due to the opponent’s mistakes anyway, are not optimal to be carried out, it seems much more efficient to think in width, i.e. all our choices and only their very basic consequences. Thinking in depth only works when the opponent has only one single optimal answer (in which case our effort is also much easier), in other words only when the opponent is in a forcing position.
Stability and natural variation of the evaluation.
If we exclude intentionally wrong moves, we have no control over our unconscious mistakes. It is therefore more consistent to evaluate after any move we make and before the opponent plays, in the sense that whatever unconscious mistake we were about to make we just made and there is no point in considering it. So suppose the opponent played the move $X$. For any sequence of optimal or non-optimal moves it holds
$$ X \geq Xa \leq XaY \geq XaYb \leq XaYbZ ... $$
where the equalities hold when optimal answers are assigned to the position given by their left term and the inequalities hold when no optimal answers are assigned. So we see that the evaluations decrease with our own errors and increase with the errors of the opponents. Without errors the evaluations seem as if they do not vary.
The only objective evaluation is at the end of the game by its result. Defeat, draw or win. We already put $0$ on the draw (here we mean a sure objective draw) and let’s adopt what we did when we first learned chess and what chess programs do today. Let’s set the unit of evaluation at $1$ a pawn. It doesn’t matter the value, so let’s set the objective final loss as $-10$ and the objective final win as $+10$. Since three are the final objective results, three are the unique objective evaluations $\{-10, 0, +10\}$. For any subjective evaluation to be meaningful when both players are playing optimally, it should, as the game progresses towards the end, converge and have the objective evaluation as the limit at the end of the game. That is, it should tend to one of three values $\{-10, 0, +10\}$. The three values of the objective evaluation act as three attractors of the subjective evaluation and so the subjective evaluation is approximated as a constant during the optimal evolution of the game but, in fact, move by move it varies slightly to arrive at one of the three attractors of the three final outcomes.
Since the subjective evaluation has one value and at the same time, with optimal play, converges to one of the three attractors, there should be two undefined but finite upper and lower bounds around the $0$ value of the draw. Suppose $-5$ and $+5$. Subjective evaluations below the lower bound of $-5$ will naturally decrease and tend to $-10$ (the sure defeat) as optimal play approaches towards the end of the game. Subjective evaluations greater than the upper bound of $+5$ will naturally increase and tend to $+10$ (the sure win) as optimal play approaches the end of the game. Subjective evaluations between the two bounds will vary naturally and will tend to $0$ (the sure draw) as optimal play approaches the end of the game.
Opponents’ errors are expected to cause much larger variations in the subjective evaluation than the natural variation from optimal play. For this reason, and because the local natural variation is small, we can approximate and consider that locally
for small sequences of optimal moves, the subjective evaluation is approximated as a constant, having zero or negligible natural variation.
Beliefs
Through the competitive subjective evaluation we compare positions and moves on the board. In fact, the comparison of positions and moves itself is what is expressed as subjective evaluation. For the same reasons that the competitive evaluation is subjective, the comparison of positions and moves can only be subjective and based on our formed beliefs. How correct our beliefs turn out to be depends on experience, study, training, knowledge of our opponent and our weaknesses, the acumen of the moment, and the like.
The correctness of the beliefs and, consequently, the correctness of the subjective evaluation is not examined at all. In this article the subjective evaluation is taken for granted. No matter how correct they are, * our beliefs ought to create a consistent logical structure, that is, they ought not to contradict each other. For this reason, this article considers a consistency of beliefs in alternative transpositions, not the correctness of those beliefs per se.
An example of belief inconsistency was already given at the end of the “fun assumption of equality of initial moves”, where the first two beliefs ruled out as false the belief that the move 1)e4 is better than 1)h3.
Another example of a consistent belief structure is the following:
- Belief 1). The difference between a strong player and his weak opponent is more evident in strategic decisions than in tactical strokes, because the strong player will more easily initiate a wrong tactical combination than make a wrong strategic decision.
- Belief 2). Games starting with 1)d4 contain more strategic decisions than tactical blows than games starting with 1)e4 which, because of their open nature and more direct contact between the two sides, contain more tactical blows than strategic decisions.
- Belief 3) As a consequence of 1) and 2). The strong player has a better chance of a positive result if he starts with 1)d4, because this will make the difference in dynamics more apparent.
- Belief 4) As a consequence of 3). I have black and my strongest opponent started with 1)e4. The move 1)e4 played by white is weaker than the move 1)d4 he could have played.
Because of the above structure, if belief 1) were reversed, its consequences, i.e. beliefs 3) and 4), would also be reversed.
In general, I believe that the beliefs of players who have studied opening and ending theory are, if not correct, certainly stronger at these stages of the game than in the middle of the game, where their beliefs may be weaker and sometimes non-existent, depending on their skills.
Reasonable alternative transpositions
Many times the same position can be obtained with a different sequence of moves. In these cases, because the same position is obtained, each alternative sequence of moves results in the same evaluation. In the simplest case, three moves are involved. Since we have no control over the unconscious error we just made with our last move, let us assume that starting from a particular position, a transitional position arises from the move sequence $XaY$, with $X, Y$ being the opponent’s moves and $a$ being our unique move. The only alternative sequence, so that, from the given starting position, the same transitional position arises at the end, is the sequence $YaX$.
For there to be an alternative transition to the same position it may be possible and necessary that the three movements be performed by different pieces, none of them blocking the movement of the other and none of the three pieces being captured by each other. But we need not prove this in the present article. For the evaluation of intermediate positions, when each of the moves, in its generality, may or may not be optimal, it holds
$$ X \geq Xa \leq XaY = YaX $$
Opposing inequalities do not help in drawing any conclusion and therefore we should eliminate the inequality concerning an opponent’s move, giving a reason for his play. This cause can only be the optimal play on his part. Let’s call these alternative transitions reasonable. The only inequality involving an opponent’s move is the second one. By converting it to equality we restrict ourselves to the sequences for which it holds that the opponent’s second move $Y$ is optimal $ Xa = XaY = Y^{Xa} $. So we consider only the cases for which
$$ X \geq Xa = XaY^{Xa} = Y^{Xa}aX \geq Y^{Xa}a $$
The last inequality holds because if $X$ is an optimal response to $Ya$ then it does not change its evaluation $YaX = Ya$. But if it is not optimal, it is better for us because it increases the evaluation of our own view $YaX > Ya$.
Consistency of beliefs in reasonable alternative transpositions.
Condensing the previous relation, and omitting the exponents of the optimal Y for simplicity, we have
For reasonable transpositions the following applies
$$ X \geq Ya $$
Following the above, let us consider the structure formed by our two plausible beliefs.
-
Belief 1) There is a reasonable transposition $XaY$, in which the opponent’s second move $Y$ is optimal.
-
Belief 2) The opponent’s first move $X$ is better than his second $Y$. This means that the position evaluation, if he plays $X$, will be worse for us than if he plays $Y$, i.e. $ X < Y $.
The evaluation of $Y$ will not change against our optimal response $b^Y$. Therefore, from our second belief,
$$ X < Yb^Y $$
So we see that if the optimal $b^Y$ were any of our $a$ answers of the reasonable transposition, i.e., if $a = b$, the last two inequalities would be in complete contradiction, since in the first case the evaluation $X$ would be greater than or equal to $Ya$ and in the second case less than $Ya$.
- ** Belief 3) as a consequence of 1) and 2)**
Reasonable transposition’s theorem:
In reasonable transpositions $XaY^{Xa}$ for which the opponent did not choose the optimal move $X$, but instead chose the inferior move $Y$, then none of our possible responses $a$ is optimal to the move $Y$.
Note that neither $X$ against the current position nor $a$ against $X$ is required to be optimal.
If the above theorem does not hold in practice, either the first belief or the second or both do not hold. In other words, formulated in reverse, the theorem would read as follows:
*If our optimal response $b^Y$ to the opponent’s move $Y$ is contained in an alternative transition $XbY$ then either the alternative transposition is not reasonable, i.e. $Y$ is not an optimal response to the moves $Xb$ or the move $X$ is not better than $Y$ or both.
Examples
The above theorem is also applicable to other chess-like games and, instead of any of the three moves, general plans or blocks of moves can be used. In these cases, however, even though the second belief may be easily formed, that is $X < Y$, it is rare and difficult to establish the first belief, i.e. that the independence required by alternative transpositions exists and that these transpositions are reasonable, i.e. that the move $Y = Y^{Xa}$ is optimal with respect to the moves $Xa$.
Let’s look at some examples.
Plans:
- Regardless of whether it is his optimal choice, the opponent can $X=$ “block the center”. After blocking the center, any $a=$ “our flanking activity” is optimal for him to respond with $Y=$ “attack the king’s wing.” We have the belief that it is better for the opponent to block the center than to launch a direct attack on the king’s wing. Instead, the opponent starts with $Y=$ “attack the king’s wing.” By the theorem, any “our flanking activity” is not an optimal response to his attack.
- If it is better for the opponent to first play an intermediate move $X$ to provoke an $a$ response from us and then play the $Y$ move he wants, but still play $Y$ first, then, without a challenge, it is not optimal for us, in response to $Y$, to play $a$.
- If we have the belief that the theory corresponds to the optimal moves but the opponent has chosen to move away from it, it is not optimal for us to choose an answer that might allow him to return. It is a non-optimal response, which many players choose because of the illusion of safety it provides.
Block:
Suppose that after 1.e4 c5 2.Nf3 e6
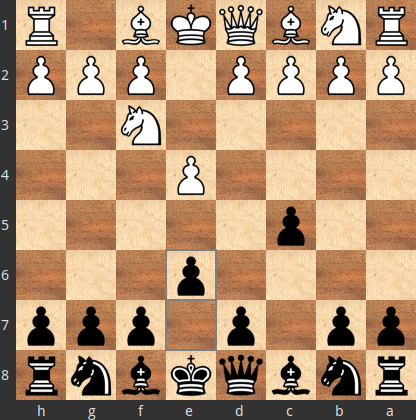
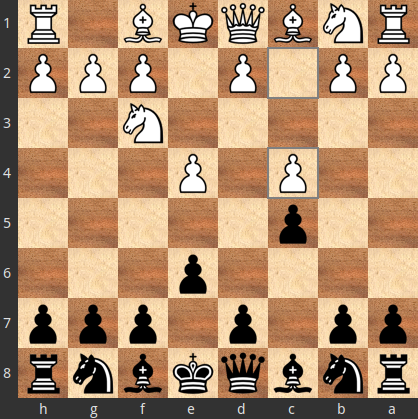
1.e4 c5 2.Nf3 e6 3.c4
The theorem seems to be unable to exclude any move from belonging to the optimal answers, because if $X=3.d4$
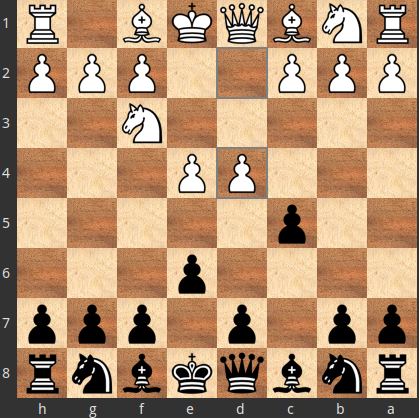

1.e4 c5 2.Nf3 e6 3.d4 cxd4 4.Nxd4
Semi-open openings with 2.d4:
Let’s follow the example of the “Beliefs” verse and
-
suppose that a stronger opponent has opened with $Y=1.e4$, while we have the belief that it would be better for him to open with $X=1.d4$. All answers $a$, such as $e6, c6, a6, g6, h6,$ which against $X=1.d4$ have $Y^{d4,a}=2.e4$ as the optimal answer, are not optimal answers to the $1.e4$ opening.
-
Suppose that a weak opponent opened with $Y=1.d4$, while we are of the belief that it would be better for him to open with $X=1.e4$. Responses corresponding to semi-open openings that have $Y^{e4,a}=2.d4$ as the optimal response are not optimal responses to the $1.d4$ opening.
The two previous examples may give the wrong impression that, when the moves 1.e4 and 1.d4 have different evaluations, the semi-open openings with optimal 2.d4 cannot be optimal in any case. But such a claim cannot be proved by the reasonable transposition’s theorem if the opponent has chosen the optimal for him, in our opinion, first move. With an additional level of abstraction, e.g. by assigning open, closed and semi-open openings to tactical, strategic and semi-strategic play (whatever the latter may mean) and classifying the opponent in either the tactical or strategic class then, against his optimal choice, the semi-strategic play appears as our optimal response.
1.e4, 1.Nf3:
If, for the opponent, $X=1.e4$ is better than $Y=1.Nf3$, but the opponent has chosen $Y=1.Nf3$, then obviously $a=1... e5$ and $a=1... c5$, which have $Y^{Xa}=2.Nf3$ as their optimal answer to $X=1.e4$, are not optimal answers to $Y=1.Nf3$.
1.d4, 1.Nf3 (absence of reasonable transposition):
If, for the opponent, $X=1.d4$ is better than $Y=1.Nf3$, but the opponent has chosen $Y=1.Nf3$, then by the theorem we cannot decide for any move of Black as to whether it belongs or not to his optimal answers. This is because, opposite 1.d4, no move of Black seems to cause 2.Nf3 as the reason for an optimal response.
- 1.d4, 1.c4:
If, for the opponent, $X=1.d4$ is better than $Y=1.c4$, but the opponent has chosen $Y=1.c4$, then moves $a$ such as 1… Nf6, d5, or f5, which against $X=1.d4$ have $Y^{Xa}=2.c4$ as their optimal response, are not optimal responses to $Y=1.c4$.
- 1.Nf3, 1.c4:
If, for the opponent, $X=1.Nf3$ is better than $Y=1.c4$, but the opponent has chosen $Y=1.c4$, then moves $a$ such as 1… Nf6, c6 or c5, which against $X=1.Nf3$ have an optimal response of $Y^{Xa}=2.c4$, are not optimal responses to $Y=1.c4$.
It goes without saying that if both 1.d4 and 1.Nf3 are better, for the opponent, than the 1.c4 he chose, the above beliefs accumulate and none of the moves 1… Nf6, d5, f5, f5, c6 or c5 is optimal response to 1.c4.
1.e4 e5 2.Nf3, 2.Bc4:
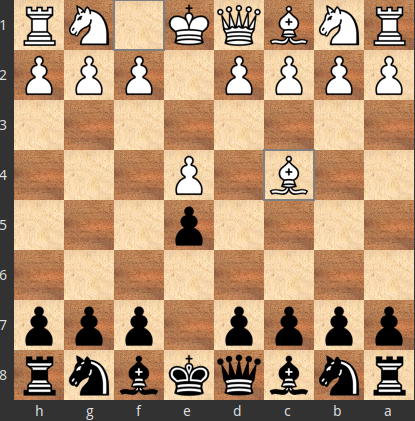
1.e4 e5 2.Bc4
If, for the opponent, $X=2.Nf3$ is better than $Y=2.Bc4$, but the lower $Y=2.Bc4$ was chosen, then $a=2... Nc6$, which opposite $X=2.Nf3$ admits $Y^{Xa}=3.Bc4$ as the optimal answer, is not an optimal answer to $Y=2.Bc4$.
1.e4 e5 2.Nf3 2…. Nc6, 2…. Nf6:
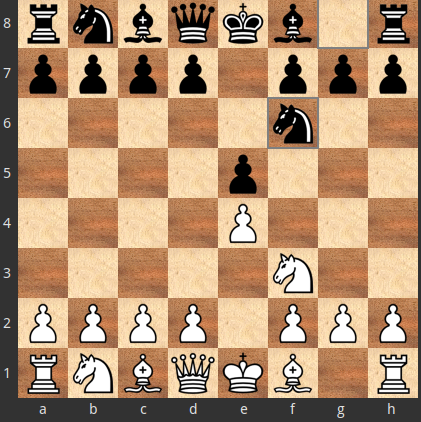
1.e4 e5 2.Nf3 Nf6
If, for the opponent, $X=2... Nc6$ is better than $Y=2... Nf6$, but the inferior $Y=2... Nf6$ was chosen, then the moves $a=3.Bc4$ and $a=3.Nc3$, which against $X=2... Nc6$ the $Y^{Xa}=3... Nf6$ is an optimal answer, are not optimal answers to $Y=2... Nf6$.
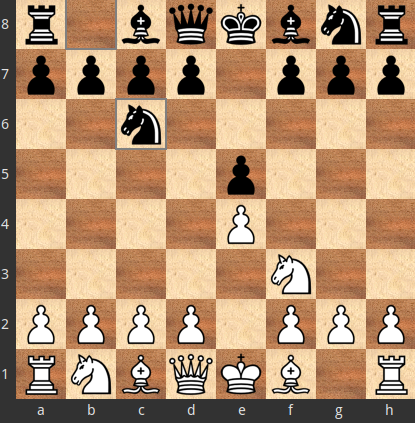
1.e4 e5 2.Nf3 Nc6
If, for the opponent, $X=2... Nf6$ is better than $Y=2... Nc6$, but the inferior $Y=2... Nc6$ was chosen, then moves such as $a=3.Nc3$, $a=3.Be2$ and $a=3.d3$, which against $X=2... Nf6$, the $Y^{Xa}=3... Nc6$ is an optimal answer, are not optimal answers to $Y=2... Nc6$.
From the two previous examples, perhaps the wrong impression is given that the move $Nc3$ cannot be optimal against any of Black’s main continuations after 1.e4 e5 2.Nf3. But such a claim cannot be proved by the reasonable transposition’s theorem, if the opponent has chosen the, in our opinion, optimal continuation for himself.
1.e4 e5 2.Nf3 Nf6 3.Bc4
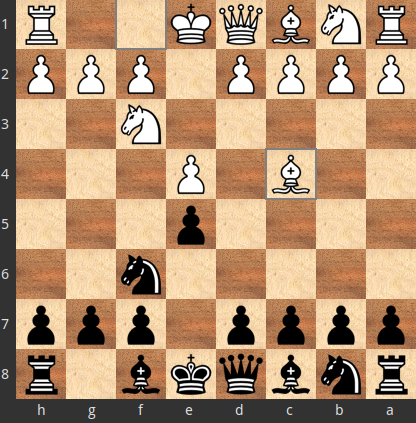
If, for the opponent, $X=3.Nxe5$ is better than $Y=3.Bc4$, but the inferior $Y=3.Bc4$ was chosen, then the move $a=3... c6$, which opposite to $X=3.Nxe5$ $Y^{Xa}=4.Bc4$ is one of the optimal answers, is not an optimal answer to $Y=3.Bc4$.
Maybe with our answer $3... Nc6$ there could be a direct transition to an optimal for us variation of the “Italian” variation 1. e4 e5 2.Nf3 Nc6 3.Bc4 Nf6, but this has nothing to do with a reasonable transposition’s theorem. The $3... Nc6$ answer, in this position, is not optimal because otherwise there would be a contradiction with our current beliefs. We have already chosen $2... Nf6$ from $2.… Nc6$, because according to our current beliefs the “Russian” 1. e4 e5 2.Nf3 Nf6 has a higher evaluation of the “Italian” 1. e4 e5 2.Nf3 Nc6. So there is a better option than allowing the “Italian” with $3... Nc6$.
1.e4 e5 2.Nf3 Nc6 3.Bb5 a6 4.Ba4 Nf6 5.0-0:
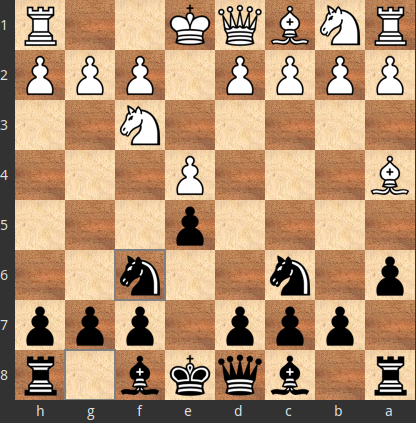
We have the belief that the optimal move at this position is $X=$5.0-0. Therefore, if the opponent plays:
Y=5.d4, our answer $a=5... Nxe4$ will not be optimal because, after $X=$5.0-0 Nxe4, $Y^{Xa}=6.d4$ is one of the optimal moves.
Y=5.Bb3, our answer $a=$5… b5$ will not be optimal because, after $X=$5.0-0 b5, $Y^{Xa}=6.Bb3$ is one of the optimal moves.
Y=5.c3, our answer $a=5… Bc5$ will not be optimal because, after $X=$5.0-0 Bc5, $Y^{Xa}=6.c3$ is one of the optimal moves.
Afterword
Whatever is better for the opponent is worse for us. The opponent’s evaluation and perspective may differ from ours. But the opponent’s perspective is completely irrelevant to the conclusions of this article. Any comparison herein refers to our own subjective evaluation.
The reasonable transposition’s theorem does not indicate optimal options. It indicates some non-optimal options, which could, for that reason, be excluded from the search for optimal options.
The basic premise for applying the theorem is that the opponent played incorrectly or otherwise non-optimally.
If the goal is to find optimal moves in the face of an opponent’s correct play, refer to chess theory or other articles on the subject.
My sincere thanks to any reader who had the interest and managed to get this far enough to read this concluding thank you.