Γνωρίστε τα μουσικά διαστήματα και τις Neo-Riemannian κινήσεις, μέσω ενός αναλογικού ρολογιού
Μετά τον κύκλο των πέμπτων και τις διατονικές, συνεχίζοντας να διαβάζω για τα θεμελιώδη της μουσικής θεωρίας, διαπιστώνω ότι το μουσικό ρολόι μπορεί να βοηθήσει στην εύκολη αναγνώριση των διαστημάτων της συνήθους μουσικής ορολογίας.
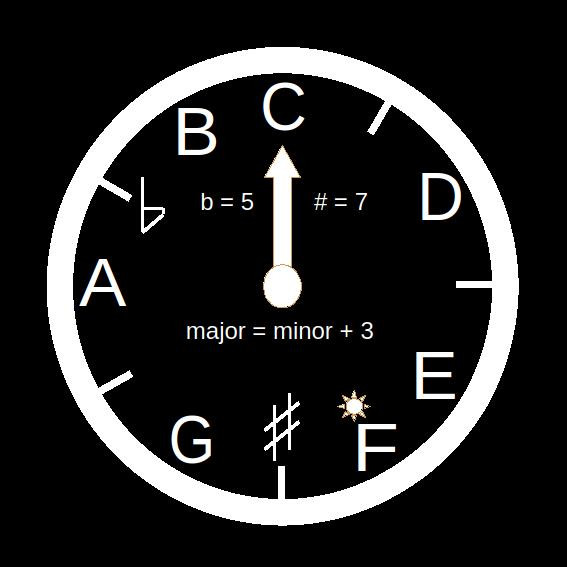
Το μουσικό ρολόι μας
Μουσικά διαστήματα
Ορολογία
Ένα μουσικό διάστημα, ως η διαφορά ανάμεσα σε δύο τονικά ύψη, μπορεί να οριστεί με απόλυτο τρόπο σαν το πλήθος των ημιτονίων που τα χωρίζουν. Το σύνολο όμως των ημιτονίων μιας οκτάβας είναι 12, ενώ οι νότες μιας κλίμακας 7. Η σχέση των τόνων σε μια μελωδία είναι αναγκαίο να εκφραστεί σαν σχέση μεταξύ των 7 τόνων της κλίμακας που χρησιμοποιείται. Έτσι, για τον καθορισμό ενός διαστήματος, είναι αναγκαίο να χρησιμοποιηθούν δύο όροι. Ο πρώτος ουσιαστικός όρος θα δείχνει την σχέση με τους 7 τόνους της κλίμακας και ο δεύτερος, ως επίθετο του πρώτου, θα προσδιορίζει το ακριβές διάστημα σε πλήθος ημιτονίων.
Μέγεθος διαστήματος
Το μέγεθος διαστήματος εκφράζει την σχέση με τις 7 νότες της κάθε κλίμακας. Είναι ο αριθμός από νότες που υπάρχουν μεταξύ της υψηλότερης νότας και της χαμηλότερης, συμπεριλαμβανομένης και της χαμηλότερης. Για αυτό το λόγο, δεν επηρεάζουν οι τονισμοί. Π.χ. το διάστημα bbE-#A έχει το ίδιο μέγεθος με το E-A, το οποίο μετρώντας E(1)-F(2)-G(3)-A(4) μας δείχνει ότι πρόκειται για 4η.
Η αντιστροφή διαστήματος
Έχουμε την αντιστροφή ενός διαστήματος όταν αντιστρέψουμε τους τόνους και ο χαμηλότερος εμφανιστεί ως ο υψηλότερος και το αντίστροφο. Π.χ. η αντιστροφή του Ε-Α είναι η Α-Ε. Επειδή το άθροισμα ενός διαστήματος και της αντιστροφής του ισούται πάντα με μία οκτάβα ή 12 ημιτόνια, (Ε-Α)+(Α-Ε)=(E-Α-Ε)=E-E, κάθε διάστημα ορίζει μονοσήμαντα την αντιστροφή του και κάθε μεταβολή (ελάττωση ή αύξηση) ενός διαστήματος ορίζει μονοσήμαντα την αντίθετη μεταβολή (αύξηση ή ελάττωση αντίστοιχα) της αντιστροφής του. Κάθε οκτάβα συμπληρώνεται μετά από 7 νότες, άρα το άθροισμα διαστήματος και της αντιστροφής του συμπληρώνεται πάντα μετά από 7 νότες. Όμως στο μέγεθος τόσο του διαστήματος όσο και της αντιστροφής του συμπεριλαμβάνουμε και την αρχική νότα τους. Έτσι, οι ονομαστικές αξίες των δύο αυτών διαστημάτων έχουν πάντα άθροισμα 7+2=9. Π.χ. εφόσον το Ε-Α είναι 4η, τότε το Α-Ε είναι (9-4=) 5η.
Επιπλέον, η αντιστροφή 6ης είναι 3η, αν αυξήσουμε μία 6η ελαττώνουμε την αντίστροφή της 3η ή αν αυξήσουμε μια 2α ελαττώνουμε την αντίστροφή της 7η κ.ο.κ.
Ποιότητα ή είδος διαστημάτων
Η ποιότητα ή το είδος κάθε διαστήματος ονομάζεται ανάλογα με τον εάν το ίδιο, ή η αντιστροφή του, ιδωμένο ως απόσταση από την τονική κάποιας κλίμακας, μπορεί να καθορίσει το είδος (μινόρε ή ματζόρε) αυτής της κλίμακας.
Επειδή ο τόνος Ντο συμβαίνει, κατά το μουσικό ρολόι, στις 00:00 η ώρα, είναι πολύ βολικό να θεωρούμε τα εξεταζόμενα διαστήματα σαν αποστάσεις από την τονική Ντο και να τα συγκρίνουμε με τις αποστάσεις των τόνων της Ντο ματζόρε. Ας δούμε τα διαστήματα από την τονική της Ντο ματζόρε (00:00 η ώρα) και τα διαστήματα από την τονική της Λα μινόρε (09:00 η ώρα).
| μέγεθος διαστήματος | (unison) 1η | 2α | 3η | 4η | 5η | 6η | 7η | (οκτάβα) 8η |
|---|---|---|---|---|---|---|---|---|
| ματζόρε κλίμακα | ||||||||
| Διάστημα από C (00:00) | 0 | 2 | 4 | 5 | 7 | 9 | 11 | 12 |
| μινόρε κλίμακα | ||||||||
| Διάστημα από Α (09:00) | 0 | 2 | 3 | 5 | 7 | 8 | 10 | 12 |
Διαπιστώνουμε ότι τα διαστήματα 3ης, 6ης και 7ης, επειδή διαφέρουν μεταξύ των ματζόρε και μινόρε κλιμάκων, άμεσα ξεχωρίζουν αν αποτελούν αποστάσεις από την τονική τους. Για αυτό:
Τα διαστήματα των 4, 9 και 11 ημιτονίων ονομάζονται 3η ματζόρε, 6η ματζόρε και 7η ματζόρε αντίστοιχα. Τα, κατά 1 ημιτόνιο, μικρότερα διαστήματα των 3, 8 και 10 ημιτονίων ονομάζονται 3η μινόρε, 6η μινόρε και 7η μινόρε αντίστοιχα.
Το διάστημα 2 ημιτονίων από την τονική, επειδή είναι κοινό και στις δύο κλίμακες, δημιουργεί αμφιβολίες ως προς την ονομασία του. Για να το ονοματίσουμε με συνέπεια πρέπει να καταφύγουμε στην 3η και 6η ή και στο ό,τι συμβαίνει στην ένωση κάθε διαστήματος με την αντιστροφή του.
Όπως προαναφέραμε, αυτή η ένωση δίδει πάντοτε απόσταση 12 ημιτονίων. Ας φανταστούμε μία φανταστική απόσταση 3½ ημιτονίων. Η αντιστροφή της θα ισούται με 8½ ημιτόνια.
Αν αυξήσουμε την πρώτη κατά ½ ημιτόνιο, για να παραμείνει το άθροισμα 12, η δεύτερη απόσταση μειώνεται κατά ½ ημιτόνιο. Η πρώτη γίνεται 4 ημιτόνια, δηλαδή 3η ματζόρε, και η δεύτερη 8 ημιτόνια, δηλαδή 6η μινόρε. Οπότε και το άθροισμα 3η ματζόρε και 6ης μινόρε ισούται με 12. Αν μειώσουμε την πρώτη κατά ½ ημιτόνιο, για να παραμείνει το άθροισμα 12, η δεύτερη απόσταση αυξάνεται κατά ½ ημιτόνιο. Η πρώτη γίνεται 3 ημιτόνια, δηλαδή 3η μινόρε, και η δεύτερη 9 ημιτόνια, δηλαδή 6η ματζόρε. Οπότε και το άθροισμα 3η μινόρε και 6ης ματζόρε ισούται με 12.
Η συνέπεια απαιτεί κάθε ματζόρε διάστημα μαζί με την μινόρε αντιστροφή του να δίδει διάστημα 12 ημιτονίων.
Με την βοήθεια της παραπάνω παρατήρησης μπορεί να προσδιοριστεί η άγνωστη 2α του διαστήματος των 2 ημιτονίων. Η αντιστροφή της ισούται με 10 ημιτόνια, τα οποία έχουν χαρακτηριστεί ήδη ως 7η μινόρε. Για την συμπλήρωση των 12 ημιτονίων η 7η μινόρε πρέπει να ενωθεί με 2η ματζόρε. Συνεπώς, το διάστημα των 2 ημιτονίων ονομάζεται 2η ματζόρε, παρόλο που είναι κοινό και στα δύο είδη κλιμάκων.
Η 4η, των 5 ημιτονίων, είναι κοινό διάστημα και στις δύο κλίμακες. Όμως, και η αντιστροφή της η 5η, των 7 ημιτονίων, είναι κοινό διάστημα και στις δύο κλίμακες. Λόγω των παραπάνω, κανείς δεν μπορεί να αποφανθεί αν οι εν λόγω αποστάσεις, της 4ης και της 5ης, από την τονική, δημιουργούνται από ματζόρε ή μινόρε κλίμακα. Άρα, δεν μπορούν να οριστούν δύο διαφορετικές κλάσεις για αυτά τα διαστήματα, παρά μόνο μία, αυτήν του τέλειου διαστήματος, αφού και οι δύο κλίμακες τις ίδιες αποστάσεις παράγουν. Το ίδιο συμβαίνει για τα διαστήματα 1ης (unison) και 8ης (οκτάβας).
Λόγω των παραπάνω, τα διαστήματα 1ης, 8ης, 4ης και 5ης ονομάζονται τέλεια διαστήματα.
Αυξημένα και ελαττωμένα διαστήματα
Έχουμε ορίσει έτσι τα μινόρε διαστήματα ώστε η αύξησή τους κατά 1 ημιτόνιο να δίδει τα ματζόρε διαστήματα. Περαιτέρω αύξηση των ματζόρε διαστημάτων κατά 1, 2, 3 κ.ο.κ. ημιτόνια, απλώς παράγει τα απλά, διπλά, τριπλά κ.ο.κ. αυξημένα διαστήματα.
Έχουμε ορίσει έτσι τα ματζόρε διαστήματα ώστε η μείωσή τους κατά 1 ημιτόνιο να δίδει τα μινόρε διαστήματα. Περαιτέρω μείωση των μινόρε διαστημάτων κατά 1, 2, 3 κ.ο.κ. ημιτόνια, απλώς παράγει τα απλά, διπλά, τριπλά κ.ο.κ. ελαττωμένα διαστήματα.
Στα τέλεια διαστήματα δεν υπάρχει διαφοροποίηση. Η αύξηση των τέλειων διαστημάτων παράγει, απευθείας, αυξημένα διαστήματα, ενώ η μείωση των τέλειων διαστημάτων παράγει, απευθείας, ελαττωμένα διαστήματα, όπως ακριβώς στα λοιπά ματζόρε ή μινόρε διαστήματα.
Αναγνώριση διαστημάτων
Η αναγνώριση των διαστημάτων γίνεται εύκολα αν συγκριθούν, με την βοήθεια του μουσικού ρολογιού, με τις αποστάσεις από την τονική της Ντο ματζόρε.
Χρειάζεται βέβαια να έχουμε απομνημονεύσει, εκτός των αυτονόητων της 1ης και 8ης, ότι τόσο η 4η, των 5 ημιτονίων (b=5), όσο και η 5η, των 7 ημιτονίων (#=7), είναι τέλεια διαστήματα. Δεν είναι δύσκολο όμως, αφού η 5η και τα 7 ημιτόνιά της (#=7) είναι γνωστό ότι παίζουν κυρίαρχο ρόλο στη θεωρία της μουσικής. Παρά το ότι είναι πασίγνωστο ότι (b + # = 12), τα συνδεδεμένα με την 4η και 5η σύμβολα ύφεσης (b) και δίεσης (#) σημειώνονται, έτσι κι αλλιώς, ως υπενθύμιση στο μουσικό ρολόι.
Η διαδικασία αναγνώρισης γίνεται ως εξής:
- Αναγνωρίζουμε από τα ονόματα των τόνων (αγνοώντας τους τονισμούς) το μέγεθος του διαστήματος.
- Διαπιστώνουμε το πλήθος των ημιτονίων αυτού του μεγέθους στην ματζόρε κλίμακα (διαφορά ωρών από την C της ώρας 00:00). Ας το ονομάσουμε διάστημα αναφοράς.
- Λαμβάνοντας υπόψη τους τονισμούς, διαπιστώνουμε την διαφορά ωρών (ημιτονίων) του υψηλότερου τόνου από τον χαμηλότερο.
- Αν η διαφορά είναι ίση με την του διαστήματος αναφοράς, τότε έχουμε ματζόρε διάστημα ή τέλειο διάστημα. Αν η διαφορά είναι άλλη από αυτήν του διαστήματος αναφοράς, τότε μεταβάλλουμε την ποιότητα ματζόρε ή τέλειου διαστήματος τόσο ώστε να εξισωθούν τα συγκρινόμενα διαστήματα.
Παραδείγματα
- F-C: F-G-A-B-C 5 τόνοι, πρόκειται για 5η, η οποία στην ματζόρε κλίμακα είναι τέλεια και διαρκεί 7 ώρες. Η διάρκεια του συγκεκριμένου διαστήματος ισούται με C(12)-F(5)=7, ίδια με του διαστήματος αναφοράς. Δεν χρειάζεται μεταβολή, το διάστημα F-C είναι τέλεια 5η, P5.
- bE-bC: E-F-G-A-B-C 6 τόνοι, πρόκειται για 6η, η οποία στην ματζόρε κλίμακα είναι ματζόρε και διαρκεί 9 ώρες. Η διάρκεια του συγκεκριμένου διαστήματος ισούται με bC(11)-bE(3)=8 ώρες (ημιτόνια). Η ματζόρε πρέπει να ελαττωθεί κατά 1, συνεπώς, το διάστημα bE-bC είναι μινόρε 6η, mi6.
- bG-E: G-A-B-C-D-E 6 τόνοι, πρόκειται για 6η, η οποία στην ματζόρε κλίμακα είναι ματζόρε και διαρκεί 9 ώρες. Η διάρκεια του συγκεκριμένου διαστήματος ισούται με E(16)-bG(6)=10 ώρες (ημιτόνια) (Από τις 6 έως τις 4 η ώρα είναι 10 ώρες). Η ματζόρε πρέπει να αυξηθεί κατά 1, συνεπώς, το διάστημα bG-E είναι αυξημένη 6η, Α6.
- G-bbE: G-A-B-C-D-E 6 τόνοι, πρόκειται για 6η, η οποία στην ματζόρε κλίμακα είναι ματζόρε και διαρκεί 9 ώρες. Η διάρκεια του συγκεκριμένου διαστήματος ισούται με bbE(14)-G(7)=7 ώρες (ημιτόνια) (Από τις 7 έως τις 2 η ώρα είναι 7 ώρες). Η ματζόρε πρέπει να ελαττωθεί κατά 2, συνεπώς, όχι μια φορά σε μινόρε αλλά μία φορά ακόμη σε ελαττωμένη. Το διάστημα G-bbE είναι ελαττωμένη 6η, d6.
- A-C-C: A-B-C-…-C 10 τόνοι, πρόκειται για 10η (7+3=10), η οποία στην ματζόρε κλίμακα, όπως η απλή 3η, είναι ματζόρε και διαρκεί 4+12=16 ώρες. Αντί του σύνθετου διαστήματος των 16 ωρών θα αναφερόμαστε στο ισοδύναμο απλό διάστημα της 3ης των 4 ωρών. Η διάρκεια του συγκεκριμένου διαστήματος, στην απλή του μορφή και αγνοώντας την επιπλέον οκτάβα, ισούται με C(12)-A(9)=3 ώρες (ημιτόνια). Η ματζόρε των 4 ωρών πρέπει να ελαττωθεί κατά 1. Συνεπώς, το διάστημα A-C-C είναι μινόρε 10η, mi10.
- bbE-bA: E-F-G-A 4 τόνοι, πρόκειται για 4η, η οποία στην ματζόρε κλίμακα είναι τέλεια και διαρκεί 5 ώρες. Η διάρκεια του συγκεκριμένου διαστήματος ισούται με bΑ(8)-bbE(2)=6 ώρες (ημιτόνια). Η ματζόρε πρέπει να αυξηθεί κατά 1. Συνεπώς, το διάστημα bbE-bA είναι αυξημένη 4η, Α4.
Προσωπικά, έχω την εντύπωση ότι η σύνταξη του παρόντος μου πρόσφερε διπλό κέρδος. Το πρώτο ότι, ακόμα και αν ξεχάσω τις λεπτομέρειες, εύκολα μπορώ να τις αναδημιουργήσω από μνήμης, με την βοήθεια το μουσικού ρολογιού. Το δεύτερο είναι η κατανόηση ότι η τρέχουσα ορολογία περιέχει περισσότερες πληροφορίες από το πλήθος των ημιτονίων που συνιστούν ένα μουσικό διάστημα. Π.χ. για το διάστημα bbE-bA, δεν αναφέρονται απλώς τα 6 ημιτόνια της έκτασής του αλλά, δηλώνοντάς το ως αυξημένη 4η και όχι σαν ελλατωμένη 5η, παρέχονται επιπλέον πληροφορίες για την σύνδεσή του με την υπόλοιπη δομή της όποιας σύνθεσης το χρησιμοποιεί.
Neo-Riemannian κινήσεις
Τα παρακάτω αφορούν στην κατανόησή μου επί του κεφαλαίου για τις κινήσεις επί των συγχορδιών τριών φωνών Neo-Riemannian.
Οι κινήσεις Neo-Riemannian αφορούν τις ομαλότερες μεταβάσεις από σύμφωνη συγχορδία σε σύμφωνη συγχορδία αντίθετης ποιότητας (από ματζόρε σε μινόρε ή από μινόρε σε ματζόρε). Συνεπώς δεν περικλείονται οι συγχορδίες με ελαττωμένη 5η, όπως π.χ. η Σι-Ρε-Φα αλλά αντ’ αυτής περικλείεται η Σι-Ρε-#Φα.
Το γεγονός ότι δεν χρησιμοποιείται η έννοια της τονικότητας, καθιστά φυσική την χρήση του μουσικού ρολογιού. Κάθε συγχορδία συμβολίζεται με την ώρα που συμβαίνει ακολουθούμενη από το σύμβολο ‘Μ’, αν είναι ματζόρε, ή το ‘μ’ αν είναι μινόρε. Π.χ. 9μ=Λα-Ντο-Μι ή 11Μ=Σι-#Ρε-#Φα.
Οι κινήσεις
Tonnetz
Οι βασικές κινήσεις, που αφορούν στην κίνηση μόνο μίας φωνής και στο διάγραμμα Tonnetz, συμβολίζονται με τα σύμβολα ‘R’, ‘L’ και ‘P’.
- P Η συγχορδία κινείται στην αντίθετη συγχορδία της ίδιας ώρας. Π.χ. (Ντο-Μι-Σολ) 0Μ-[P]-0μ (Ντο-bΜι-Σολ).
- Οι ματζόρε συγχορδίες (με 4-3 διαστήματα ημιτονίων) μπορούν να κινηθούν στις αντίθετης ποιότητας συγχορδίες είτε 3 ώρες νωρίτερα (κίνηση R) είτε 4 ώρες αργότερα (κίνηση L). Π.χ. (Ντο-Μι-Σολ) 0Μ-[R]-9μ (Λα-Ντο-Μι) ή (Ντο-Μι-Σολ) 0Μ-[L]-4μ (Μι-Σολ-Σι)
- Οι μινόρε συγχορδίες (με 3-4 διαστήματα ημιτονίων) μπορούν να κινηθούν στις αντίθετης ποιότητας συγχορδίες είτε 4 ώρες νωρίτερα (κίνηση L) είτε 3 ώρες αργότερα (κίνηση R). Π.χ. (Ντο-bΜι-Σολ) 0μ-[L]-8Μ (bΛα-Ντο-bΜι) ή (Ντο-bΜι-Σολ) 0μ-[R]-3Μ (bΜι-Σολ-bΣι).
Ένας άλλος εύκολος τρόπος είναι να απομνημονεύσετε ότι η ρίζα των μείζονων συγχορδιών μπορεί να μετακινηθεί σε μια ρίζα μια μείζονα τρίτη ψηλότερα (ή μια μινόρε τρίτη χαμηλότερα) και η ρίζα των μινόρε συγχορδιών μπορεί να μετακινηθεί σε μια ρίζα μια μινόρε τρίτη ψηλότερα (ή μια μείζονα τρίτη χαμηλότερα).
Το διάγραμμα Tonnetz περιγράφει γραφικά τις προαναφερόμενες κινήσεις.
Cube dance
Η κίνηση R είναι η μόνη που κινεί την μία φωνή κατά έναν τόνο αντί για ημιτόνιο. Αν, προς την κατεύθυνση της R, εισάγουμε την κίνηση ημιτόνιου, καταλήγουμε ενδιάμεσα σε αυξημένη συγχορδία. Τις αυξημένες συγχορδίες τις συμβολίζω με τις ώρες των τόνων των φωνών, π.χ. [0:4:8] = Ντο-Μι-#Σολ. Η ενδιάμεση συγχορδία είναι ίδιας ώρας με την ματζόρε της R κίνησης και 3 ώρες μεταγενέστερη της μινόρε. Πλεονέκτημα αποκτάται από το γεγονός ότι η αυξημένη συγχορδία είναι απόλυτα συμμετρική, οπότε, εκτός του προορισμού της R, η κατάληξη μπορεί να γίνει και στους λοιπούς δύο χρόνους που αντιστοιχούν στις υπόλοιπες φωνές της αυξημένης συγχορδίας.
Παραδείγματος χάριν, η κίνηση (Ντο-Μι-Σολ) 0Μ-[R]-9μ (Λα-Ντο-Μι) αναπτύσσεται ως (Ντο-Μι-Σολ) 0Μ - [0:4:8] (Ντο-Μι-#Σολ) - 9μ (Λα-Ντο-Μι), που είναι η κατάληξη 3 ώρες νωρίτερα της ώρας 0. Μπορεί όμως, εξίσου ομαλά, να καταλήξει σε μινόρε 3 ώρες νωρίτερα των 8 (ώρα που ανήκει στην αυξημένη [0:4:8]). Έτσι, να έχουμε την νέα κίνηση (Ντο-Μι-Σολ) 0Μ - [4:8:0] (Μι-bΛα-Ντο) - 1μ (bΡε-Φα-bΛα).
Προσωπικές σημειώσεις επί του συγκεκριμένου προαναφερόμενου κεφαλαίου, στην αγγλική, βρίσκονται σε pdf.
Υστερόγραφο
Εκτεταμένη χρήση του μουσικού ρολογιού, αναφερόμενο ως ‘clock face’, εμφανίζεται στο κεφάλαιο VIII Τεχνικές του 20ου και 21ου αιώνα του πολύ καλού διαδικτυακού βιβλίου μουσικής θεωρίας “OPEN MUSIC THEORY”. Επειδή όμως το προαναφερόμενο κεφάλαιο αναφέρεται σε μεθοδολογίες μουσικής ανάλυσης μέσω της μαθηματικής θεωρίας συνόλων (μην τρομάζετε! όπως γνωρίζετε τα ρολόγια, γνωρίζετε και τα σύνολα), το μουσικό ρολόι χρησιμοποιείται ως παραστατικό εργαλείο ανάλυσης ‘ατονικής’ μουσικής, χωρίς αναφορά σε τονικότητες, άρα χωρίς αναφορά στις υπογραφές κλειδιών, όπου κυρίως το χρησιμοποιήσαμε.
(Σημαντική αναφορά: Λίγους μήνες μετά την συγγραφή του παρόντος, ήρθε υπόψη μου η εκπληκτική, από κάθε άποψη, ιστοσελίδα Ολοκληρωμένη θεωρία μουσικής της οποίας δεν θα μπορούσα να παραλείψω την αναφορά της).