Σκάκι: Συνέπεια πεποιθήσεων στις εναλλακτικές μεταβάσεις
Στρατηγική εναντίον του παιγνιδιού.
Για υπερβολικά μεγάλο χρονικό διάστημα έπαιζα παρτίδες εναντίον του ιδίου του παιγνιδιού. Θεωρούσα δηλαδή ότι, αντικειμενικά και ανεξαρτήτως αντιπάλου, υπάρχει βέλτιστη στρατηγική δια της οποίας επιτυγχάνεται νίκη. Το ζητούμενο, είτε σε μελέτη είτε σε αγώνα, ήταν να βρεθεί αυτή η στρατηγική. Αυτή η θεώρηση δημιουργούσε μεγάλη πίεση για εύρεση βέλτιστης κίνησης και συγχρόνως αδικαιολόγητη απογοήτευση όταν ένα όποιο πλεονέκτημα θέσης δεν ήταν δυνατόν να υλοποιηθεί.
Όταν κάποιος υπερυπολογιστής λύσει το παιγνίδι, κάθε θέση θα μπορεί να αντιστοιχηθεί στους αριθμούς {-1, 0, 1} ανάλογα με το αποτέλεσμα στο οποίο θα καταλήγει το βέλτιστο παίξιμο και των δύο πλευρών. Τότε θα υπάρχει αντικειμενική αξιολόγηση ακόμα και της αρχικής θέσης.
Όταν παίζουμε εναντίον του παιγνιδιού, παραδεχόμαστε εμμέσως ότι υπάρχει νικηφόρα πλευρά και αναζητούμε την στρατηγικής της, κατά την οποία επιλέγονται μόνον κινήσεις που καταλήγουν σε θέσεις με την αντικειμενική αξιολόγηση του πρόσημου της νίκης. Ακόμα όμως και αν υπάρχει αντικειμενική αξιολόγηση που οδηγεί σε στρατηγική νίκης, ψάχνοντάς την, εύκολα παραγνωρίζουμε ότι η μη νικηφόρα πλευρά, εξ ανάγκης, βασίζει την βέλτιστη στρατηγική της σε υποκειμενική αξιολόγηση της θέσης.
Η πλευρά που ηττάται, αν γνωρίζει τον άνθρωπο αντίπαλό της, οφείλει να επιλέξει θέσεις όπου η πιθανότητα λάθους από αυτόν είναι αυξημένη. Αν δεν τον γνωρίζει, οφείλει να επιλέξει θέσεις όπου η πιθανότητα λάθους από τον ίδιο είναι ελαττωμένη. Συνήθως δε οφείλει να το πράξει συγχρόνως, επιλέγοντας θέσεις όπου η πιθανότητα μεγαλύτερου λάθους από τον αντίπαλο, παρά από τον ίδιο, είναι αυξημένη. Συνεπώς, η πλευρά που ηττάται, σε κάθε συγκεκριμένη θέση, εξαρτά τις βέλτιστες κινήσεις της από τον αντίπαλο που αντιμετωπίζει καθώς και από τις εφήμερες ή μόνιμες ίδιες αδυναμίες της.
Υποκειμενική αξιολόγηση θέσης
Αξίωμα βέλτιστης επιλογής
Αξιωματικά δεχόμαστε ότι, μετά την επιλογή του χρώματος με το οποίο θα παίξει κάθε παίκτης, η κάθε παρτίδα εξελίσσεται με επιλογές βέλτιστων κινήσεων και από τους δύο αντιπάλους.
Το παραπάνω αξίωμα είναι αυτονόητο για οποιαδήποτε ορθολογική ανάλυση. Φιλτράρει όμως εκτός ανάλυσης κάθε παρτίδα που περιέχει μη ορθολογικές κινήσεις. Αν π.χ. άγνωστος αντίπαλος εκκινήσει με 1.)e4 και πιστεύουμε ότι η απάντηση 1)… e5 είναι ισχυρότερη της 1)… c5 τότε, με βάση το αξίωμα της βέλτιστης επιλογής, οφείλουμε να απαντήσουμε με 1)… e5. Περιπτώσεις όπως της επιλογής της 1)… c5 ως απάντησης, επειδή απλά βαρεθήκαμε να απαντάμε με 1)… e5, είναι εκτός ορθολογικού πλαισίου και, ως εκ τούτου, δεν είναι αντικείμενα του παρόντος άρθρου.
Παραδοχή ισόπαλου αποτελέσματος
Παρακολουθώντας το παίξιμο των πανίσχυρων πλέον σκακιστικών προγραμμάτων, σχετικά εύκολα μπορούμε να υιοθετήσουμε την παραδοχή ότι, με βέλτιστη στρατηγική του μαύρου απέναντι σε βέλτιστη στρατηγική του λευκού, το αποτέλεσμα κάθε παρτίδας είναι ισοπαλία.
Κάθε θέση που προέρχεται από βέλτιστο παίξιμο έχει ως αντικειμενική αξιολόγηση την ισοπαλία. Έτσι, αν επιτυγχάνουμε βέλτιστο παίξιμο, η όποια νίκη μας εξαρτάται αποκλειστικά από τα λάθη του αντιπάλου, ενώ η ήττα μας, αν ο αντίπαλος παίζει βέλτιστα, εξαρτάται αποκλειστικά από τα δικά μας λάθη.
Το πόσα και ποια λάθη θα κάνει κάθε παίκτης δεν εξαρτάται αντικειμενικά από τους κανόνες του παιγνιδιού. Ως εκ τούτου, η ύπαρξη λαθών εξαρτάται από τους εκάστοτε αντιπάλους, άρα η όποια εκτίμηση ως προς τα λάθη που θα υπάρξουν δεν μπορεί παρά να είναι υποκειμενική.
Για να κατανοηθεί περισσότερο η έννοια της υποκειμενικότητας της αξιολόγησης, που εξαρτάται τόσο από εμάς όσο και από τον αντίπαλο, ας υποθέσουμε ότι, όταν παίζουμε με τα λευκά εναντίον ισοδυνάμου αντιπάλου, η αξιολόγηση της αρχικής θέσης εκφράζεται με το ότι “τα λευκά έχουν την πρωτοβουλία”. Όταν παίζουμε με τον παγκόσμιο πρωταθλητή, η αξιολόγηση της ίδιας αρχικής θέσης εκφράζεται με το ότι “τα μαύρα κερδίζουν”.
Η αξιολόγηση των κινήσεων που παρατηρούμε στην ανάλυση των σκακιστικών μηχανών είναι και αυτή υποκειμενική. Είναι αξιολόγηση που βασίζεται στον αντίπαλό τους και, εν προκειμένω, αξιολογούν θεωρώντας ότι παίζουν εναντίον του εαυτού τους. Ό,τι κάνουν και οι άνθρωποι παίκτες δηλαδή κατά την ανάλυσή τους, μόνον που οι σκακιστικές μηχανές είναι πολλαπλώς πιο ισχυρές από τους ανθρώπους.
Η αντικειμενική αξιολόγηση κάθε θέσης προέρχεται από βέλτιστο παίξιμο και δεν μπορεί να είναι χρήσιμη σε σκακιστικούς αγώνες, διότι κάθε τέτοια θέση, βέλτιστου παιξίματος, αξιολογείται σταθερά ως ισοπαλία. Μόνη χρήσιμη αξιολόγηση κάθε θέσης σε σκακιστικούς αγώνες είναι όποια υποκειμενική αξιολόγηση εκτιμά την πιθανότητα ύπαρξης λαθών από τους παίκτες, οπότε και δεν εξαρτάται από τους κανόνες του παιγνιδιού.
Συμπερασματικά, η χρήσιμη για σκακιστικούς αγώνες αξιολόγηση είναι υποκειμενική και εκτιμά τα λάθη που μπορεί να υπάρξουν στην συνέχεια της παρτίδας.
Το παιγνίδι του σκακιού έχει σήμερα δύο υποστάσεις. Την υπόσταση της αναζήτησης των αντικειμενικά βέλτιστων κινήσεων, δια της σκακιστικής θεωρίας που αναπτύσσεται επί τούτου, και την αγωνιστική υπόσταση. Η τελευταία βασίζεται στα ανθρώπινα λάθη των αντιπάλων και τις υποκειμενικές αξιολογήσεις κατά την διάρκεια των αγώνων. Όταν σημάνει το τέλος του παιγνιδιού ως σκακιστική θεωρία, δηλαδή όταν το παιγνίδι επιλυθεί πλήρως από μελλοντικούς υπέρ υπολογιστές, τότε το σκάκι θα αποτελεί πλέον καθαρό αγώνισμα, όπως τα περισσότερα αγωνίσματα, όπου άνθρωποι αντίπαλοι θα ανταγωνίζονται στις αρετές που η φύση του σκακιού απαιτεί.
Διασκεδαστική παραδοχή ισότητας αρχικών κινήσεων
Η παραδοχή ισόπαλου αποτελέσματος αρκεί για να καταδείξει την χρησιμότητα της υποκειμενικής αξιολόγησης από μόνη της. Φαντάζει όμως διασκεδαστικό το να υιοθετήσουμε επιπλέον την άποψη ότι είναι προτιμότερο να παιχθεί οποιαδήποτε αρχική κίνηση των λευκών παρά να επιλεχθούν τα μαύρα.
Λόγω της παραδοχής ισόπαλου αποτελέσματος, το καλύτερο αποτέλεσμα που μπορεί να επιτύχει ο λευκός απέναντι στις βέλτιστες απαντήσεις του μαύρου είναι η ισοπαλία.
Το να επιλέξει κάποιος παίκτης τα μαύρα είναι ισοδύναμο με το να επιτρέπουν οι κανονισμοί στον λευκό να μην εκκινήσει με καμία εκ των 20 αρχικών κινήσεων, δηλαδή με κάποια από το ζεύγος των επιτρεπόμενων κινήσεων κάθε πιονιού ή ίππου, αλλά να παραχωρήσει το προνόμιο της πρώτης κίνησης στον μαύρο. Ήδη δεχθήκαμε όμως ότι αυτή είναι η χειρότερη αρχική επιλογή ενός παίκτη. Συνεπώς, μετά από την χείριστη επιλογή του χρώματος των μαύρων, το αποτέλεσμα είναι και πάλι η ισοπαλία.
Εφόσον το καλύτερο αποτέλεσμα του λευκού είναι η ισοπαλία και το χειρότερο, παραχωρώντας το προνόμιο της πρώτης κίνησης, είναι και πάλι η ισοπαλία, τότε κάθε μία από τις 20 αρχικές κινήσεις του αξιολογείται αντικειμενικά ως ισοπαλία. Άρα όλες οι 20 αρχικές κινήσεις του λευκού είναι αντικειμενικά ισάξιες.
Το διασκεδαστικό του πράγματος, αναφερόμενο στα προηγούμενα, είναι ότι δεν μπορεί κάποιος να δέχεται α) ότι είναι καλύτερο να παιχθεί οποιαδήποτε κίνηση των λευκών παρά να επιλεχθούν τα μαύρα, β) ότι τα μαύρα μπορούν να επιτύχουν ισοπαλία και, συγχρόνως, να ισχυρίζεται γ) ότι η εκκίνηση π.χ. με 1)e4 είναι αντικειμενικά καλύτερη της εκκίνησης με 1)h3. H 1)ε4 μπορεί να είναι καλύτερη της 1)h3 μόνον υποκειμενικά, επειδή π.χ. ο αντίπαλος είναι άνθρωπος και αναμένεται να κάνει περισσότερα λάθη αντιμετωπίζοντας την 1)e4 παρά την 1)h3.
Ιδιότητες υποκειμενικής αξιολόγησης.
Συμβολισμοί
Ας θεωρήσουμε την αξιολόγηση ως συνάρτηση, των δυνατών σκακιστικών θέσεων, επί των φυσικών αριθμών. Δεν έχει σημασία σε ποιους φυσικούς αριθμούς αντιστοιχίζονται οι θέσεις. Σημασία έχει η σύγκριση θέσεων να αντιστοιχεί σε σύγκριση αριθμών. Ας εκφράζεται λοιπόν η αξιολόγηση των θέσεων πλήρους ισότητας με τον αριθμό $0$. Θέσεις όπου, στην συνέχεια, αναμένονται περισσότερα ή/και μεγαλύτερα λάθη από τον αντίπαλο, παρά από εμάς, θα έχουν θετική αξιολόγηση. Στην αντίθετη περίπτωση, όπου εμείς, και όχι αντίπαλος, αναμένεται να κάνουμε περισσότερα ή/και μεγαλύτερα λάθη, η αξιολόγηση θα είναι αρνητική.
Ας συμβολίσουμε, για λόγους οικονομίας συμβολισμών, με $X$ τόσο την θέση που προκύπτει μετά την κίνηση $X$ όσο και την αξιολόγησή της. (Πιστεύω ότι από τα συμφραζόμενα θα είναι κατανοητό ποιος από τους δύο συμβολισμούς είναι σε ισχύ.) Τότε με $Χa$ συμβολίζουμε τόσο την θέση που προκύπτει μετά την απάντηση $a$ στην κίνηση $X$ όσο και την αξιολόγησή της. Η $a$, σε αυτόν τον συμβολισμό μπορεί να είναι ή και να μην είναι βέλτιστη απάντηση στην $X$. Aν $a$ είναι βέλτιστη απάντηση στην κίνηση $X$, τότε την θέση, ή την αξιολόγηση της θέσης που προκύπτει, ας την συμβολίσουμε με $a^X$, θέτοντας στον εκθέτη την θέση επί της οποίας η κίνηση βάσης $a$ είναι βέλτιστη.
Εφόσον η υποκειμενική αξιολόγηση εκτιμά τα λάθη που θα συμβούν στην συνέχεια της παρτίδας και αυτά τα λάθη διαπιστώνονται συγκρινόμενα σχετικά με το βέλτιστο παίξιμο, εξ ανάγκης, η αξιολόγηση θέσεων που προέρχονται από ακολουθίες βέλτιστων κινήσεων δεν αλλάζει αλλά παραμένει σταθερή.
Έτσι, όταν μετά την κίνηση $X$ έχουμε βέλτιστες συνέχειες, θα ισχύει, ως προς τις αξιολογήσεις,
$$ X = a^{X} = Y^{a^X} = b^{Y^{a^X}} = Z^{b^{Y^{a^X}}} = ... $$
όπου, στο παραπάνω, παιχτήκαν κατά σειρά οι κινήσεις $X, a, Y, b, Z$, με όλες, εκτός της αδιευκρίνιστης πρώτης $X$, να είναι βέλτιστες κινήσεις.
Ίσως αποδειχθεί χρήσιμο να ορίσουμε ως μπλοκ μιας κίνησης $Χ$, όπως $ \{ XaY \} $ ή $ \{ XaYbZ \} $, διατηρώντας τον ίδιο συμβολισμό $X$, μια ακολουθία βέλτιστων κινήσεων μετά την οποία είναι η σειρά του επόμενου παίκτη να απαντήσει. Εννοείται πως η αξιολόγηση παραμένει ίδια είτε μετά την κίνηση $X$ είτε μετά από μπλοκ της κίνησης $X$. Παρά την σύγχυση λόγω της χρήσης ίδιου συμβολισμού για την θέση, κίνηση, μπλοκ κίνησης ή την αξιολόγησή της, πρέπει να είναι καθαρό ότι για τις αξιολογήσεις των μπλοκ ισχύει
$$ X = \{ XaY \}=Y^{a^X}=\{ XaYbZ \}= Z^{b^{Y^{a^X}}} $$
Επειδή το μπλοκ κινήσεων χρησιμοποιεί βέλτιστες κινήσεις εννοείται ότι εξαρτάται από την θέση στην οποία παρουσιάζεται. Οι ίδια ακολουθία κινήσεων μπορεί να είναι μπλοκ σε μία θέση και να μην είναι σε μία άλλη, διότι απλούστατα τα μέλη της ακολουθίας δεν αποτελούν βέλτιστες κινήσεις στη νέα θέση.
Η σταθερότητα της αξιολόγησης ενός μακροσκελούς μπλοκ βέλτιστων κινήσεων δεν είναι απόλυτη. Ισχύει μόνον προσεγγιστικά, όπως θα δούμε στο μεθεπόμενο εδάφιο.
Συσσώρευση λαθών
Η, εξ ανάγκης υποκειμενική όπως προαναφέραμε, αξιολόγηση της θέσης εκτιμά τα λάθη που θα γίνουν στην συνέχεια της παρτίδας. Έστω $a$ κίνησή μας στην οποία ο αντίπαλος απαντά με $Y$. Αν η $Y$ είναι βέλτιστη τότε η αξιολόγηση, εκ της $a$, θα παραμείνει σταθερή και θα ισχύει $ a = aY = Y^a$. Αν όμως δεν είναι βέλτιστη, ο αντίπαλος έκανε λάθος οπότε η αξιολόγηση θα αυξηθεί και θα ισχύει $ a < aY $. Αν συνεχίσουμε με βέλτιστη $b$ η αξιολόγηση δεν θα αλλάξει, οπότε θα ισχύει $ a < aY = aYb = b^{aY}$. Αν ο αντίπαλος ανταπαντήσει με μη βέλτιστη κίνηση $Z$, κάνοντας πάλι λάθος δηλαδή, η αξιολόγηση θα αυξηθεί ακόμα περισσότερο και θα ισχύει $ a < aY = aYb < aYbZ$.
Βλέπουμε λοιπόν ότι απέναντι σε βέλτιστο παίξιμο, τα λάθη του αντιπάλου (ή τα δικά μας) τείνουν να συσσωρεύονται. Τι ακριβώς όμως σημαίνει βέλτιστο παίξιμο απέναντι στα λάθη του αντιπάλου; Σημαίνει ότι προηγείται το λάθος του αντιπάλου που αύξησε την αξιολόγηση και ότι, στην συνέχεια, η βέλτιστη απάντηση σε αυτό το λάθος απλώς διατηρεί την υποκειμενική αξιολόγηση στο αυξημένο επίπεδο που την βρήκε και δεν την αυξάνει.
Παραδείγματος χάριν, έστω ότι ο αντίπαλος με την κίνηση $Y$ εγκατέλειψε μια κάθετο ή δημιούργησε ένα αδύνατο τετράγωνο κ.λ.π. και για αυτό τον λόγο ανέβασε την αξιολόγηση. Για να κατοχυρώσουμε την αυξημένη αξιολόγηση, πρέπει να παίξουμε βέλτιστη κίνηση $b$, κατακτώντας έτσι την κάθετη ή το αδύνατο τετράγωνο κ.λ.π., αλλιώς, αν παίξουμε λάθος, η αυξημένη αξιολόγηση θα μειωθεί. Αν ο αντίπαλος με το λάθος του δεν είχε αυξήσει την αξιολόγηση δεν θα είχαμε την ευκαιρία να κατακτήσουμε κάθετη ή αδύνατο τετράγωνο κ.λ.π. και έτσι δεν θα βελτιώναμε τη θέση μας.
Η αύξηση της αξιολόγησης προηγείται της βελτίωσης θέσεων.
Συνεπώς, με βέλτιστο παίξιμο, συσσωρεύονται τα πλεονεκτήματα που κατακτώνται, όπως ακριβώς θεωρούσε ο Steinitz, αλλά αυτό συμβαίνει μόνον εφόσον συσσωρεύονται τα λάθη του αντιπάλου, αυξάνοντας την αξιολόγηση. Με αυτήν την έννοια, δεν είναι η κατάκτηση στρατηγικών πλεονεκτημάτων, όπως η κατοχή καθέτου ή αδύνατου τετραγώνου, προϋπόθεση του βέλτιστου παιξίματος αλλά το βέλτιστο παίξιμο, απέναντι στα λάθη του αντιπάλου, είναι η προϋπόθεση της κατάκτησης στρατηγικών πλεονεκτημάτων.
Η στρατηγική δεινότητα δεν έγκειται στην κατάκτηση στρατηγικών πλεονεκτημάτων αλλά στην ανίχνευση αύξησης της αξιολόγησης, λόγω των λαθών του αντιπάλου, και την προσαρμογή μας σε αυτήν με βέλτιστο παίξιμο. Π.χ. πρώτα ανιχνεύεται αύξηση αξιολόγησης λόγω εγκατάλειψης καθέτου και ύστερα το βέλτιστο παίξιμό μας πιθανώς να οδηγήσει στην κατάκτησή της.
Η παραπάνω οπτική φαίνεται να έχει επίπτωση στον τρόπο που αντιλαμβανόμαστε την στρατηγική. Πολλές φορές, κατά τη διάρκεια της παρτίδας και κατά κόρον κατά την επιλογή ανοιγμάτων ή βαριάντας, φαίνεται ότι έχουμε να επιλέξουμε μεταξύ πολλών βέλτιστων κινήσεων. Κάθε μία από αυτές τις βέλτιστες κινήσεις πιθανώς οδηγεί σε διαφορετική κατεύθυνση την παρτίδα. Το γεγονός αυτό δίδει την ψευδαίσθηση ότι μπορούμε να εκπονούμε μακρόχρονα σχέδια και να κατευθύνουμε την παρτίδα σύμφωνα με ένα γενικό πλάνο που έχουμε κατά νου. Όμως, όποιο σχέδιο ή γενικό πλάνο επιλέξουμε βασίζεται στις βέλτιστες απαντήσεις του αντιπάλου. Έτσι, από μία ισόπαλη θέση, ακολουθώντας ένα γενικό πλάνο θα καταλήξουμε σε ισοπαλία, εφόσον ο αντίπαλος επιλέγει μεταξύ βέλτιστων κινήσεων. Παρά την επιλογή βέλτιστου πλάνου, δεν υπάρχει τρόπος να κερδίσουμε την παρτίδα απέναντι σε βέλτιστο παίξιμο.
Αν όμως ο αντίπαλος, σε κάποια κίνησή του, αυξήσει την αξιολόγηση διαπράττοντας λάθος, τότε πρέπει να είμαστε ψυχολογικά έτοιμοι να εγκαταλείψουμε το πλάνο μας, να προσαρμοστούμε στην νέα αυξημένη αξιολόγηση και να κατευθυνθούμε όπου το λάθος του αντιπάλου μας επιβάλει. Αν επιμείνουμε να ακολουθούμε το μη επίκαιρο πλέον πλάνο μας, μπορεί όχι μόνον να μην κερδίσουμε την παρτίδα αλλά και να την χάσουμε.
Είναι καλό να ξέρουμε που βρισκόμαστε ακολουθώντας βέλτιστα πλάνα αλλά πρέπει να τα εγκαταλείπουμε τόσες φορές όσα και τα λάθη του αντιπάλου. Όταν αντιμετωπίζουμε λοιπόν έναν αδύνατο αντίπαλο, που κάνει συνεχώς λάθη, δεν μπορούμε να ακολουθούμε μακρόχρονα πλάνα και να ισχυριζόμαστε, συγχρόνως, ότι παίζουμε βέλτιστα. Καλύτερα μετά από κάθε κίνηση του αντιπάλου, ειδικά όταν είναι μη αναμενόμενη άρα μη βέλτιστη άρα λανθασμένη, να αναδημιουργούμε εξ αρχής νέα σχέδια.
Αντί να ξοδεύουμε αγωνιστικό χρόνο σκεπτόμενοι εις βάθος, δηλαδή μια επιλογή σε βάθος αρκετών κινήσεων, εκ των οποίων οι δικές μας, έτσι κι αλλιώς λόγω των λαθών του αντιπάλου, δεν είναι βέλτιστο να πραγματοποιηθούν, φαίνεται πολύ πιο αποδοτικό να σκεφτόμαστε εις πλάτος, δηλαδή όλες μας τις επιλογές και μόνον τις πολύ βασικές επιπτώσεις τους. Η σκέψη εις βάθος αποδίδει μόνον όταν ο αντίπαλος έχει μοναδική βέλτιστη απάντηση (οπότε η προσπάθειά μας είναι και πολύ πιο εύκολη) ή αλλιώς μόνον όταν ο αντίπαλος βρίσκεται σε θέση φορσέ.
Σταθερότητα και φυσική μεταβολή της αξιολόγησης.
Αν αποκλείσουμε τις ηθελημένα λανθασμένες κινήσεις, δεν έχουμε έλεγχο επί των ασυνείδητων λαθών μας. Είναι λοιπόν πιο συνεπές η αξιολόγηση να γίνεται μετά την όποια κίνησή μας και πριν να παίξει ο αντίπαλος, με την έννοια του ότι ό,τι ασυνείδητο λάθος ήταν να κάνουμε μόλις το κάναμε και δεν έχει νόημα να το λάβουμε υπόψη. Έστω λοιπόν ότι ο αντίπαλος έπαιξε την κίνηση $X$. Για κάθε ακολουθία βέλτιστων ή μη κινήσεων ισχύει
$$ X \geq Xa \leq XaY \geq XaYb \leq XaYbZ ... $$
όπου οι ισότητες ισχύουν όταν δίδονται βέλτιστες απαντήσεις στην θέση που δίδεται από τον αριστερό τους όρο και οι ανισότητες ισχύουν όταν δεν δίνονται βέλτιστες απαντήσεις. Βλέπουμε λοιπόν ότι οι αξιολογήσεις μειώνονται με τα λάθη τα δικά μας και αυξάνονται με τα λάθη των αντιπάλων. Χωρίς λάθη οι αξιολογήσεις φαίνεται σαν να μην μεταβάλλονται.
Η μόνη αντικειμενική αξιολόγηση υπάρχει στο τέλος της παρτίδας δια του αποτελέσματός της. Ήττα, ισοπαλία ή νίκη. Θέσαμε ήδη $0$ στην ισοπαλία (εδώ εννοούμε την σίγουρη αντικειμενική ισοπαλία) και ας υιοθετήσουμε ό,τι κάναμε όταν πρωτομαθαίναμε σκάκι και ό,τι κάνουν τα σκακιστικά προγράμματα σήμερα. Ας θέσουμε ως μονάδα αξιολόγησης $1$ το ένα πιόνι. Δεν έχει σημασία η τιμή, για αυτό ας θέσουμε την αντικειμενική τελική ήττα ως $-10$ και την αντικειμενική τελική νίκη ως $+10$. Εφόσον τρία είναι τα τελικά αντικειμενικά αποτελέσματα, τρεις είναι και οι μοναδικές αντικειμενικές αξιολογήσεις $\{-10, 0, +10\}$. Για να έχει νόημα η όποια υποκειμενική αξιολόγηση όταν και οι δύο παίκτες παίζουν βέλτιστα, θα πρέπει, όσο προχωράει η παρτίδα προς το τέλος της, να συγκλίνει και να έχει όριο στο τέλος της παρτίδας την αντικειμενική αξιολόγηση. Να τείνει δηλαδή σε μία από τις τρεις τιμές $\{-10, 0, +10\}$. Οι τρεις τιμές της αντικειμενικής αξιολόγησης λειτουργούν σαν τρεις ελκυστές της υποκειμενικής αξιολόγησης και έτσι η υποκειμενική αξιολόγηση προσεγγίζεται μεν ως σταθερά κατά την βέλτιστη εξέλιξη της παρτίδας αλλά, για την ακρίβεια, κίνηση με την κίνηση μεταβάλλεται ελαφρά, ώστε να καταλήξει σε έναν από τους τρεις ελκυστές των τριών τελικών αποτελεσμάτων.
Εφόσον η υποκειμενική αξιολόγηση έχει μία τιμή και ταυτόχρονα, με βέλτιστο παίξιμο, συγκλίνει σε έναν από τους τρεις ελκυστές, θα πρέπει να υπάρχουν δύο απροσδιόριστα μεν αλλά πεπερασμένα δε άνω και κάτω φράγματα γύρω από την τιμή $0$ της ισοπαλίας. Ας υποθέσουμε τα $-5$ και $+5$. Υποκειμενικές αξιολογήσεις μικρότερες του κάτω φράγματος $-5$ Θα μειώνονται φυσικά και θα τείνουν στο $-10$ (την σίγουρη ήττα) όσο το βέλτιστο παίξιμο πλησιάζει προς το τέλος της παρτίδας. Υποκειμενικές αξιολογήσεις μεγαλύτερες του πάνω φράγματος $+5$ Θα αυξάνονται φυσικά και θα τείνουν στο $+10$ (την σίγουρη νίκη) όσο το βέλτιστο παίξιμο πλησιάζει προς το τέλος της παρτίδας. Υποκειμενικές αξιολογήσεις ανάμεσα στα δύο φράγματα θα μεταβάλλονται φυσικά και θα τείνουν στο $0$ (την σίγουρη ισοπαλία) όσο το βέλτιστο παίξιμο πλησιάζει προς το τέλος της παρτίδας.
Τα λάθη των αντιπάλων είναι φυσικό να προκαλούν πολύ μεγαλύτερες αυξομειώσεις στην υποκειμενική αξιολόγηση από ό,τι προκαλεί η φυσική μεταβολή της από το βέλτιστο παίξιμο. Για αυτό και επειδή η τοπική φυσική μεταβολή είναι μικρή, μπορούμε να προσεγγίζουμε και να θεωρούμε ότι τοπικά, δηλαδή
για μικρές ακολουθίες βέλτιστων κινήσεων, η υποκειμενική αξιολόγηση προσεγγίζεται ως σταθερά, έχοντας μηδενική ή αμελητέα φυσική μεταβολή.
Πεποιθήσεις
Δια της αγωνιστικής υποκειμενικής αξιολόγησης συγκρίνουμε θέσεις και κινήσεις επί της σκακιέρας. Για την ακρίβεια η ίδια η σύγκριση θέσεων και κινήσεων είναι αυτό που εκφράζεται ως υποκειμενική αξιολόγηση. Για τους ίδιους λόγους που η αγωνιστική αξιολόγηση είναι υποκειμενική, η σύγκριση θέσεων και κινήσεων δεν μπορεί παρά να είναι υποκειμενική και να βασίζεται σε διαμορφωμένες πεποιθήσεις μας. Το πόσο ορθές θα αποδεικνύονται οι πεποιθήσεις μας εξαρτάται από την εμπειρία, την μελέτη, την προπόνηση, την γνώση του αντιπάλου και των αδυναμιών μας, την οξυδέρκεια της στιγμής και άλλα παρόμοια.
Ουδόλως εξετάζεται η ορθότητα των πεποιθήσεων και, κατά συνέπεια, η ορθότητα της υποκειμενικής αξιολόγησης. Στο παρόν άρθρο η υποκειμενική αξιολόγηση θεωρείται δεδομένη. Ανεξάρτητα όμως από το πόσο ορθές είναι, οι πεποιθήσεις μας οφείλουν να δημιουργούν μία συνεπή λογική δομή, δηλαδή να μην έρχονται σε αντίθεση μεταξύ τους. Γι αυτό το λόγο, το παρόν άρθρο εξετάζει μια συνέπεια πεποιθήσεων στις εναλλακτικές μεταβάσεις και όχι την ορθότητα των πεποιθήσεων αυτών καθ’ εαυτών.
Ένα παράδειγμα ασυνέπειας πεποιθήσεων δόθηκε ήδη στο τέλος του εδαφίου της “διασκεδαστικής παραδοχής ισότητας αρχικών κινήσεων”, όπου οι δύο πρώτες πεποιθήσεις απέκλειαν ως εσφαλμένη την πεποίθηση ότι η κίνηση 1)e4 είναι καλύτερη της 1)h3.
Ένα άλλο παράδειγμα συνεπούς δομής πεποιθήσεων είναι το εξής:
- Πεποίθηση 1). Η διαφορά ενός δυνατού παίκτη από τον αδύνατο αντίπαλό του είναι περισσότερο εμφανής στις στρατηγικές αποφάσεις παρά στα τακτικά κτυπήματα, διότι ο δυνατός παίκτης θα εκκινήσει πιο εύκολα λανθασμένο τακτικό συνδυασμό παρά θα πάρει λανθασμένη στρατηγική απόφαση.
- Πεποίθηση 2). Οι παρτίδες που εκκινούν με 1)d4 περιέχουν περισσότερες στρατηγικές αποφάσεις, παρά τακτικά κτυπήματα, από τις παρτίδες που εκκινούν με 1)e4 που, λόγω του ανοικτού χαρακτήρα τους και της πιο άμεσης επαφής των δύο πλευρών, περιέχουν περισσότερα τακτικά κτυπήματα, παρά στρατηγικές αποφάσεις.
- Πεποίθηση 3) Ως συνέπεια των 1) και 2). Ο δυνατός παίκτης έχει καλύτερες πιθανότητες θετικού αποτελέσματος αν ξεκινήσει με 1)d4, διότι έτσι θα γίνει πιο εμφανής η διαφορά δυναμικότητας.
- Πεποίθηση 4) Ως συνέπεια της 3). Έχω τα μαύρα και ο δυνατότερος αντίπαλός μου ξεκίνησε με 1)e4. H κίνηση 1)e4 που παίχτηκε από τον λευκό είναι πιο αδύνατη από την κίνηση 1)d4 που θα μπορούσε να παίξει.
Λόγω της παραπάνω δομής, αν αντιστρεφόταν η πεποίθηση 1) θα αντιστρεφόταν και οι συνέπειές της, δηλαδή οι πεποιθήσεις 3) και 4).
Γενικά, πιστεύω, ότι οι πεποιθήσεις παικτών που έχουν μελετήσει θεωρία ανοιγμάτων και φινάλε, είναι, αν όχι ορθές, σίγουρα πιο ισχυρές σε αυτά τα στάδια της παρτίδας από ό,τι στο μέσον της, όπου οι πεποιθήσεις τους μπορεί να είναι πιο ισχνές και μερικές φορές ανύπαρκτες, ανάλογα με τις ικανότητες του καθενός.
Αιτιώδεις εναλλακτικές μεταβάσεις
Πολλές φορές η ίδια θέση μπορεί να προκύψει με διαφορετική σειρά κινήσεων. Στις περιπτώσεις αυτές, επειδή προκύπτει η ίδια θέση, κάθε εναλλακτική ακολουθία κινήσεων καταλήγει στην ίδια αξιολόγηση. Στην πιο απλή περίπτωση εμπλέκονται τρεις κινήσεις. Αφού δεν έχουμε έλεγχο επί του ασυνείδητου λάθους που μόλις πράξαμε με την τελευταία μας κίνηση, ας θεωρήσουμε ότι εκκινώντας από μια συγκεκριμένη θέση προκύπτει μεταβατική θέση από τη σειρά κινήσεων $XaY$, με $X, Y$ κινήσεις του αντιπάλου και $a$ τη δική μας μοναδική κίνηση. Η μόνη εναλλακτική ακολουθία, ώστε, από την συγκεκριμένη θέση εκκίνησης, να προκύψει στο τέλος η ίδια μεταβατική θέση, είναι η ακολουθία $YaX$.
Για να υπάρχει εναλλακτική μετάβαση στην ίδια θέση ίσως είναι ικανό και αναγκαίο τις τρεις κινήσεις να τις εκτελούν διαφορετικά κομμάτια, κανένα να μην εμποδίζει την κίνηση του άλλου και σε καμία από τις τρεις κινήσεις να μην συλλαμβάνονται μεταξύ τους. Αλλά δεν χρειάζεται να αποδείξουμε κάτι τέτοιο στο παρόν άρθρο. Για την αξιολόγηση των ενδιάμεσων θέσεων, όταν κάθε μία από τις κινήσεις, στην γενικότητά της, μπορεί να είναι ή και να μην είναι βέλτιστη, ισχύει
$$ X \geq Xa \leq XaY = YaX $$
Οι αντίθετες ανισότητες δεν βοηθούν στην εξαγωγή οποιουδήποτε συμπεράσματος και για αυτό θα πρέπει να εξαλείψουμε την ανισότητα που αφορά σε κίνηση του αντιπάλου, δίδοντας αιτία στο παίξιμό του. Αυτή η αιτία δεν μπορεί παρά να είναι το βέλτιστο παίξιμο από την μεριά του. Ας ονομάσουμε αυτές τις εναλλακτικές μεταβάσεις αιτιώδεις. Η μόνη ανισότητα που αφορά σε κίνηση του αντιπάλου είναι η δεύτερη. Μετατρέποντάς την σε ισότητα περιοριζόμαστε στις ακολουθίες για τις οποίες ισχύει ότι η δεύτερη κίνηση $Y$ του αντιπάλου είναι βέλτιστη $ Xa = XaY = Y^{Xa} $. Οπότε εξετάζουμε μόνον τις περιπτώσεις για τις οποίες ισχύει
$$ X \geq Xa = XaY^{Xa} = Y^{Xa}aX \geq Y^{Xa}a $$
Η τελευταία ανισότητα ισχύει διότι αν η $X$ είναι βέλτιστη απάντηση στην θέση $Ya$ τότε δεν μεταβάλλει την αξιολόγησή της $YaX = Ya$. Αν όμως δεν είναι βέλτιστη, καλύτερα για μας, διότι αυξάνει την αξιολόγηση της δικιάς μας οπτικής $YaX > Ya$.
Συνέπεια πεποιθήσεων στις αιτιώδεις εναλλακτικές μεταβάσεις.
Συμπυκνώνοντας την προηγούμενη σχέση, και παραλείποντας τους εκθέτες της βέλτιστης Υ για απλότητα, έχουμε ότι
Για τις αιτιώδεις μεταβάσεις ισχύει
$$ X \geq Ya $$
Κατόπιν των παραπάνω, ας εξετάσουμε την δομή που σχηματίζεται από δύο εύλογες πεποιθήσεις μας.
-
Πεποίθηση 1) Υπάρχει αιτιώδης μετάβαση $XaY$, κατά την οποία η δεύτερη κίνηση $Y$ του αντιπάλου είναι βέλτιστη.
-
Πεποίθηση 2) Η πρώτη κίνηση $X$ του αντιπάλου είναι καλύτερη της δεύτερης $Y$ για τον ίδιο. Αυτό σημαίνει ότι η αξιολόγηση της θέσης, αν παίξει $X$, θα είναι χειρότερη για εμάς, παρά το από αν παίξει $Y$, δηλαδή $ X < Y $.
Η αξιολόγηση της $Y$ δεν θα αλλάξει απέναντι σε βέλτιστη απάντησή μας $b^Y$. Συνεπώς, εκ της δεύτερης πεποίθησής μας,
$$ X < Yb^Y $$
Βλέπουμε λοιπόν ότι αν η βέλτιστη $b^Y$ ήταν κάποια από τις $a$ απαντήσεις μας, της αιτιώδους μετάβασης, δηλαδή αν $ a = b $, οι δύο τελευταίες ανισότητες θα έρχονταν σε πλήρη αντίθεση, αφού στην πρώτη περίπτωση η αξιολόγηση $X$ θα ήταν μεγαλύτερη ή ίση του $Ya$ και στην δεύτερη μικρότερή του.
- Πεποίθηση 3) ως συνέπεια των 1) και 2)
Θεώρημα αιτιωδών μεταβάσεων:
Στις αιτιώδεις μεταβάσεις $XaY^{Xa}$ για τις οποίες ο αντίπαλος δεν επέλεξε την βέλτιστη για τον ίδιο κίνηση $X$, αλλά, αντιθέτως, επέλεξε την κατώτερη $Y$, τότε καμία από τις τυχόν απαντήσεις μας $a$ δεν είναι βέλτιστη απάντηση απέναντι στην κίνηση $Y$.
Ας τονιστεί ότι ούτε η $X$ απέναντι στην τρέχουσα θέση ούτε η $a$ απέναντι στην $X$ απαιτείται να είναι βέλτιστες.
Αν στην πράξη δεν ισχύει το παραπάνω θεώρημα, είτε η πρώτη πεποίθησή μας είτε η δεύτερη είτε και οι δύο δεν ισχύουν. Αντίστροφα διατυπωμένο δηλαδή το θεώρημα θα είχε ως εξής:
Αν η βέλτιστη απάντησή μας $b^Y$ στην κίνηση $Y$ του αντιπάλου εμπεριέχεται σε εναλλακτική μετάβαση $XbY$ τότε είτε η εναλλακτική μετάβαση δεν είναι αιτιώδης, δηλαδή η $Y$ δεν είναι βέλτιστη απάντηση στις κινήσεις $Xb$ είτε η κίνηση $X$ δεν είναι καλύτερη της $Y$ είτε και τα δύο.
Παραδείγματα
Το παραπάνω θεώρημα είναι εφαρμόσιμο και σε άλλα παρόμοια με το σκάκι παιγνίδια και, αντί όποιας εκ των τριών κινήσεων, μπορούν να χρησιμοποιηθούν γενικά πλάνα σχεδίων ή μπλοκ κινήσεων. Σε αυτές τις περιπτώσεις όμως, ακόμα και αν μπορεί η δεύτερη πεποίθηση να διαμορφώνεται εύκολα, ότι δηλαδή $X < Y$, είναι σπάνιο και δύσκολο να δημιουργηθεί η πρώτη πεποίθηση, ότι δηλαδή υπάρχει η ανεξαρτησία που απαιτούν οι εναλλακτικές μεταβάσεις και ότι αυτές οι μεταβάσεις είναι αιτιώδεις, ότι δηλαδή η κίνηση $Y = Y^{Xa}$ είναι βέλτιστη απέναντι στις κινήσεις $Xa$.
Ας δούμε μερικά παραδείγματα.
Σχέδια:
- Ανεξάρτητα από το αν είναι βέλτιστη επιλογή του, ο αντίπαλος μπορεί $X=$ “να μπλοκάρει το κέντρο”. Μετά το μπλοκάρισμα του κέντρου, οποιαδήποτε $a=$ “πλευρική δραστηριότητά μας” είναι βέλτιστο για αυτόν να απαντηθεί με $Y=$ “επίθεση στην πτέρυγα του βασιλιά.” Έχουμε την πεποίθηση ότι είναι καλύτερο για τον αντίπαλο να μπλοκάρει το κέντρο, από το να ξεκινήσει άμεση επίθεση στην πτέρυγα του βασιλιά. Αντ’ αυτού, ο αντίπαλος ξεκινά με $Y=$ “επίθεση στην πτέρυγα του βασιλιά.” Με βάση το θεώρημα, οποιαδήποτε “πλευρική δραστηριότητά μας” δεν αποτελεί βέλτιστη απάντηση στην επίθεσή του.
- Αν είναι καλύτερο για τον αντίπαλο πρώτα να παίξει μια ενδιάμεση κίνηση $X$ για να προκαλέσει μια αντίδρασή μας $a$ και μετά να παίξει την κίνηση $Y$ που επιθυμεί, αλλά παρόλα αυτά παίξει πρώτα την $Y$, τότε, χωρίς πρόκληση δεν είναι βέλτιστο για μας, ως απάντηση στην $Υ$, να παίξουμε την κίνηση $a$.
- Αν έχουμε την πεποίθηση ότι η θεωρία αντιστοιχεί στις βέλτιστες κινήσεις αλλά ο αντίπαλος επέλεξε να απομακρυνθεί από αυτήν, δεν είναι βέλτιστο για εμάς να επιλέξουμε απάντηση που μπορεί να του δώσει την δυνατότητα να επιστρέψει. Πρόκειται για μη βέλτιστη απάντηση, που πολλοί παίκτες επιλέγουν λόγω της ψευδαίσθησης ασφάλειας που παρέχει.
Μπλοκ:
Έστω ότι μετά από 1.e4 c5 2.Nf3 e6
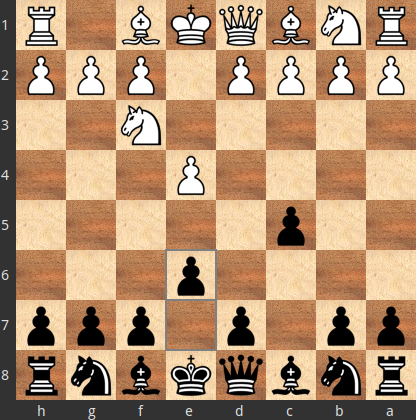
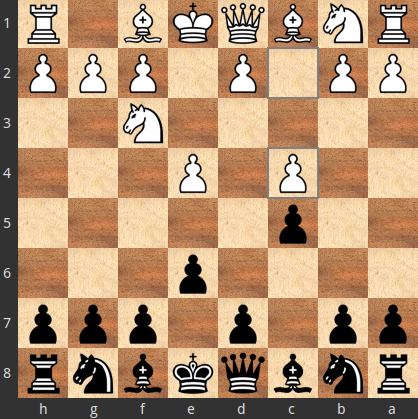
1.e4 c5 2.Nf3 e6 3.c4
Το θεώρημα φαίνεται να μην μπορεί να αποκλείσει καμία κίνηση από το να ανήκει στις βέλτιστες απαντήσεις, διότι αν είχε παιχτεί η $X=3.d4$
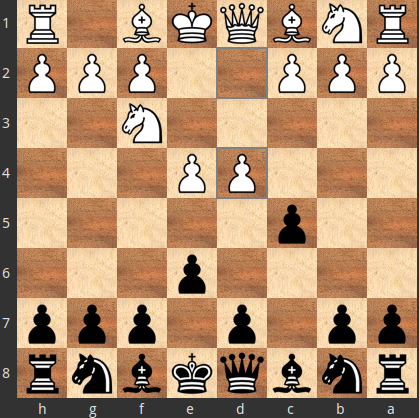

1.e4 c5 2.Nf3 e6 3.d4 cxd4 4.Nxd4
Ημιάνοικτα ανοίγματα με 2.d4:
Ας ακολουθήσουμε το παράδειγμα του εδαφίου “Πεποιθήσεις” και
-
ας υποθέσουμε ότι δυνατότερος αντίπαλος άνοιξε με $Y=1.e4$, ενώ έχουμε την πεποίθηση ότι θα ήταν καλύτερα, για τον ίδιο, να ανοίξει με $X=1.d4$. Όλες οι απαντήσεις $a$, όπως $e6, c6, a6, g6, h6$, που απέναντι στο $X=1.d4$ έχουν σαν βέλτιστη απάντηση την $Υ^{d4,a}=2.e4$, δεν είναι βέλτιστες απαντήσεις στο άνοιγμα $1.e4$.
-
Ας υποθέσουμε ότι αδύνατος αντίπαλος άνοιξε με $Y=1.d4$, ενώ έχουμε την πεποίθηση ότι θα ήταν καλύτερα, για τον ίδιο, να ανοίξει με $X=1.e4$. Οι απαντήσεις που αντιστοιχούν σε ημιάνοικτα ανοίγματα που έχουν σαν βέλτιστη απάντηση την $Υ^{e4,a}=2.d4$ δεν είναι βέλτιστες απαντήσεις στο άνοιγμα $1.d4$.
Από τα δύο προηγούμενα παραδείγματα, ίσως δίδεται η λανθασμένη εντύπωση ότι, όταν οι κινήσεις 1.e4 και 1.d4 έχουν διαφορετική αξιολόγηση, τα ημιάνοικτα ανοίγματα με βέλτιστη 2.d4, σε κάθε περίπτωση δεν μπορεί να είναι βέλτιστα. Ένας τέτοιος ισχυρισμός όμως δεν μπορεί να αποδειχθεί από το θεώρημα της αιτιώδους μετάβασης, εάν ο αντίπαλος επέλεξε την, κατά τη γνώμη μας, βέλτιστη για τον ίδιο πρώτη κίνηση. Με ένα επιπλέον επίπεδο αφαίρεσης, π.χ. αντιστοιχώντας τα ανοιχτά, κλειστά και ημιάνοικτα ανοίγματα σε τακτικό, στρατηγικό και ημιστρατηγικό παιγνίδι (ό,τι μπορεί να σημαίνει το τελευταίο) και κατατάσσοντας τον αντίπαλο είτε στην τακτική είτε στην στρατηγική κατηγορία τότε, απέναντι στην βέλτιστη επιλογή του, το ημιστρατηγικό παιγνίδι φαίνεται ως η βέλτιστη απόκρισή μας.
1.e4, 1.Nf3:
Αν, για τον αντίπαλο, είναι καλύτερο το $X=1.e4$ από το $Y=1.Nf3$, αλλά ο αντίπαλος επέλεξε $Y=1.Nf3$, τότε προφανώς η $a=1... e5$ αλλά και η $a=1... c5$, που απέναντι στην $X=1.e4$ έχουν βέλτιστη απάντηση την $Y^{Xa}=2.Nf3$, δεν είναι βέλτιστες απαντήσεις στην $Y=1.Nf3$.
1.d4, 1.Nf3 (απουσία αιτιώδους μετάβασης):
Αν, για τον αντίπαλο, είναι καλύτερο το $X=1.d4$ από το $Y=1.Nf3$, αλλά ο αντίπαλος επέλεξε $Y=1.Nf3$, τότε δια του θεωρήματος δεν μπορούμε να αποφανθούμε για καμία κίνηση του μαύρου ως προς το αν ανήκει ή δεν ανήκει στις βέλτιστες απαντήσεις του. Αυτό συμβαίνει διότι, απέναντι στην 1.d4, καμία κίνηση του μαύρου δεν φαίνεται να προκαλεί ως αιτία βέλτιστης ανταπάντησης την 2.Nf3.
- 1.d4, 1.c4:
Αν, για τον αντίπαλο, είναι καλύτερο το $X=1.d4$ από το $Y=1.c4$, αλλά ο αντίπαλος επέλεξε $Y=1.c4$, τότε κινήσεις $a$ όπως η 1… Nf6, d5, ή f5, που απέναντι στην $X=1.d4$ έχουν βέλτιστη απάντηση την $Y^{Xa}=2.c4$, δεν είναι βέλτιστες απαντήσεις στην $Y=1.c4$.
- 1.Nf3, 1.c4:
Αν, για τον αντίπαλο, είναι καλύτερο το $X=1.Nf3$ από το $Y=1.c4$, αλλά ο αντίπαλος επέλεξε $Y=1.c4$, τότε κινήσεις $a$ όπως η 1… Nf6, c6 ή c5, που απέναντι στην $X=1.Nf3$ έχουν βέλτιστη απάντηση την $Y^{Xa}=2.c4$, δεν είναι βέλτιστες απαντήσεις στην $Υ=1.c4$.
Εννοείται πως αν τόσο η 1.d4 όσο και η 1.Nf3 είναι καλύτερες, για τον αντίπαλο, από την 1.c4 που επέλεξε, οι παραπάνω πεποιθήσεις συσσωρεύονται και καμία από τις κινήσεις 1… Nf6, d5, f5, c6 ή c5 δεν είναι βέλτιστη απάντηση στην 1.c4.
1.e4 e5 2.Nf3, 2.Bc4:
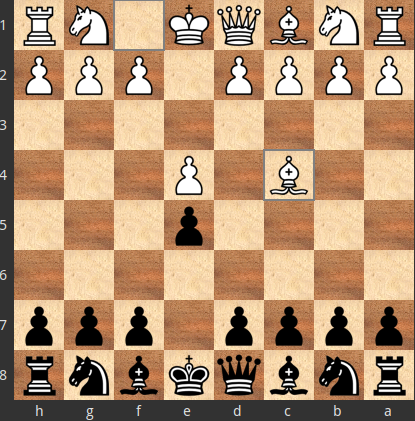
1.e4 e5 2.Bc4
Αν, για τον αντίπαλο, είναι καλύτερο το $X=2.Nf3$ από το $Y=2.Bc4$, αλλά επιλέχθηκε το κατώτερο $Y=2.Bc4$, τότε η $a=2... Nc6$, που απέναντι στην $X=2.Nf3$ η $Y^{Xa}=3.Bc4$ είναι εκ των βέλτιστων απαντήσεων, δεν είναι βέλτιστη απάντηση στην $Y=2.Bc4$.
1.e4 e5 2.Nf3 2…. Nc6, 2…. Nf6:
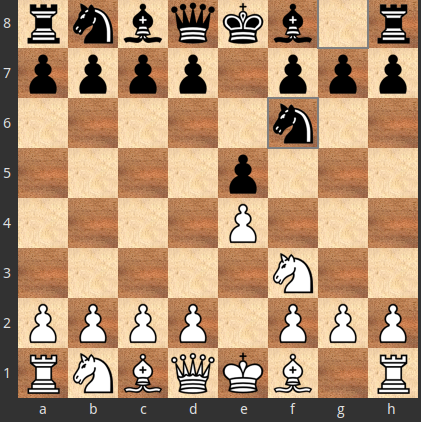
1.e4 e5 2.Nf3 Nf6
Αν, για τον αντίπαλο, είναι καλύτερο το $X=2... Nc6$ από το $Y=2... Nf6$, αλλά επιλέχθηκε το κατώτερο $Y=2... Nf6$, τότε οι κινήσεις $a=3.Bc4$ και $a=3.Nc3$, που απέναντι στην $X=2... Nc6$ η $Y^{Xa}=3... Nf6$ είναι εκ των βέλτιστων απαντήσεων, δεν είναι βέλτιστες απαντήσεις στην $Y=2... Nf6$.
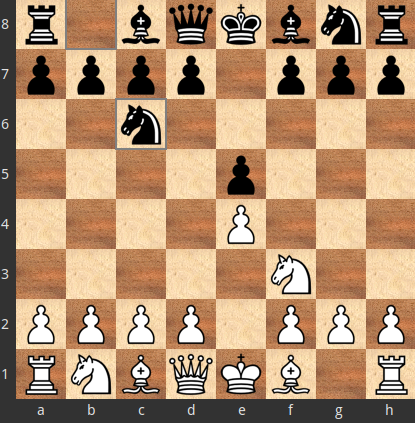
1.e4 e5 2.Nf3 Nc6
Αν, για τον αντίπαλο, είναι καλύτερο το $X=2... Nf6$ από το $Y=2... Nc6$, αλλά επιλέχθηκε το κατώτερο $Y=2... Nc6$, τότε κινήσεις όπως $a=3.Nc3$, $a=3.Be2$ και $a=3.d3$, που απέναντι στην $X=2... Nf6$ η $Y^{Xa}=3... Nc6$ είναι εκ των βέλτιστων απαντήσεων, δεν είναι βέλτιστες απαντήσεις στην $Y=2... Nc6$.
Από τα δύο προηγούμενα παραδείγματα, ίσως δίδεται η λανθασμένη εντύπωση ότι η κίνηση $Nc3$ δεν μπορεί να είναι βέλτιστη απέναντι σε καμία από τις κύριες συνέχειες του μαύρου μετά το 1.e4 e5 2.Nf3. Ένας τέτοιος ισχυρισμός όμως δεν μπορεί να αποδειχθεί από το θεώρημα της αιτιώδους μετάβασης, εάν ο αντίπαλος επέλεξε την, κατά τη γνώμη μας, βέλτιστη για τον ίδιο συνέχεια.
1.e4 e5 2.Nf3 Nf6 3.Bc4
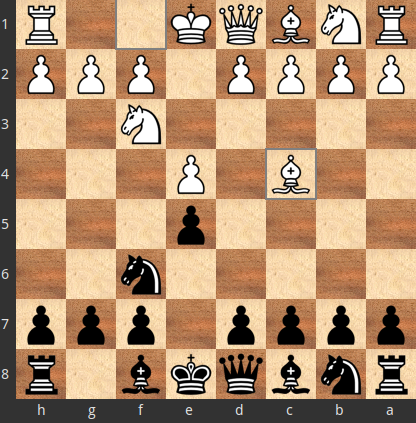
Αν, για τον αντίπαλο, είναι καλύτερο το $X=3.Nxe5$ από το $Y=3.Bc4$, αλλά επιλέχθηκε το κατώτερο $Y=3.Bc4$, τότε η κίνηση $a=3... c6$ που, απέναντι στην $X=3.Nxe5$, η $Y^{Xa}=4.Bc4$ είναι εκ των βέλτιστων απαντήσεων, δεν είναι βέλτιστη απάντηση στην $Y=3.Bc4$.
Μπορεί με την απάντησή μας $3... Nc6$ να υπάρχει απευθείας μετάβαση σε βέλτιστη για εμάς βαριάντα της “Ιταλικής” 1. e4 e5 2.Nf3 Nc6 3.Bc4 Nf6, αλλά αυτό δεν έχει σχέση με αιτιώδη μετάβαση. Η $3... Nc6$ απάντηση, σε αυτήν την θέση, δεν είναι βέλτιστη διότι αλλιώς θα υπήρχε αντίθεση με τις τρέχουσες πεποιθήσεις μας. Επιλέξαμε ήδη την $2... Nf6$ από την $2... Nc6$, διότι κατά τις τρέχουσες πεποιθήσεις μας η “ρωσική” 1. e4 e5 2.Nf3 Nf6 έχει μεγαλύτερη αξιολόγηση της “Ιταλικής” 1. e4 e5 2.Nf3 Nc6. Άρα υπάρχει καλύτερη επιλογή από το επιτρέψουμε την “Ιταλική” με $3... Νc6$.
1.e4 e5 2.Nf3 Nc6 3.Bb5 a6 4.Ba4 Nf6 5.0-0:
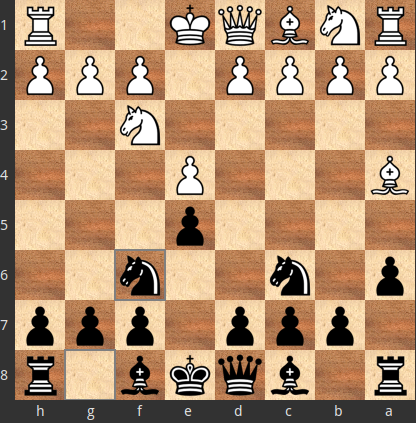
Έχουμε την πεποίθηση ότι η βέλτιστη κίνηση σε αυτήν την θέση είναι η $X=$5.0-0. Συνεπώς, αν ο αντίπαλος παίξει:
Y=5.d4, η απάντησή μας $a=5... Nxe4$ δεν θα είναι βέλτιστη διότι, στην συνέχεια $X=$5.0-0 Nxe4, η $Y^{Xa}=6.d4$ είναι μία από τις βέλτιστες κινήσεις.
Y=5.Bb3, η απάντησή μας $a=5... b5$ δεν θα είναι βέλτιστη διότι, στην συνέχεια $X=$5.0-0 b5, η $Y^{Xa}=6.Bb3$ είναι μία από τις βέλτιστες κινήσεις.
Y=5.c3, η απάντησή μας $a=5... Bc5$ δεν θα είναι βέλτιστη διότι, στην συνέχεια $X=$5.0-0 Bc5, η $Y^{Xa}=6.c3$ είναι μία από τις βέλτιστες κινήσεις.
Επίλογος
Ό,τι είναι καλύτερο για τον αντίπαλο είναι χειρότερο για εμάς. Η αξιολόγηση και η οπτική που έχει ο αντίπαλος μπορεί να διαφέρει από την δική μας. Η οπτική του αντιπάλου όμως είναι τελείως άσχετη με τα συμπεράσματα του παρόντος άρθρου. Κάθε σύγκριση στο παρόν αναφέρεται στην δική μας υποκειμενική αξιολόγηση.
Το θεώρημα της αιτιώδους μετάβασης δεν υποδεικνύει τις βέλτιστες επιλογές. Υποδεικνύει κάποιες μη βέλτιστες επιλογές, που θα μπορούσαν, για αυτό τον λόγο, να αποκλειστούν από την έρευνα για βέλτιστες επιλογές.
Βασική προϋπόθεση εφαρμογής του θεωρήματος είναι ο αντίπαλος να έπαιξε λανθασμένα ή αλλιώς μη βέλτιστα.
Αν στόχος είναι η εύρεση βέλτιστων κινήσεων απέναντι σε ορθό παίξιμο του αντιπάλου, ανατρέξτε στην σκακιστική θεωρία ή σε άλλα επί τούτου άρθρα.
Ευχαριστώ θερμά όποιον αναγνώστη είχε το ενδιαφέρον και κατάφερε να φτάσει μέχρι εδώ, ώστε να διαβάζει την παρούσα καταληκτική ευχαριστία μου.